ビジネスに役立つ統計分析の方法まとめ

目次
この記事を読んだ人がよくダウンロードする資料2つ(無料)

ビジネスにおけるデータ分析の重要性
ビジネスを成長させていくうえで、データ分析は非常に重要です。
データを収集、整理、分析し、その結果をもとに意思決定を行うことが出来るようになれば、経営者の経験に頼った経営から脱却し、客観的な指標にもとづいた経営ができるようになるからです。
データ分析には、データマイニング、統計分析、機械学習など、さまざまな種類があります。
なかでも統計分析は、データを解析し、それを使って課題の発見や経営戦略などを考えていく場合に役立ちます。
今回の記事では、統計学の入門書にも載っているような基本となる統計分析のなかで、特にビジネスに役立つと思われるものをピックアップしてご紹介します。
ビジネスで使える基本的な統計分析の種類
まず、基本的な統計分析を大きく分けると、「差の検定」と「関連性の分析」に分けることが出来ます。
「差の検定」では、グループ間の平均値の差が有意なものかどうかを検定する手法で、2グループの場合はt検定を、3グループ以上の場合は分散分析を使います。
一方、関連性の分析では、基本的な分析として、相関分析、回帰分析、カイ二乗検定などがあげられます。
ここまでをまとめると、以下の図の通りとなります。
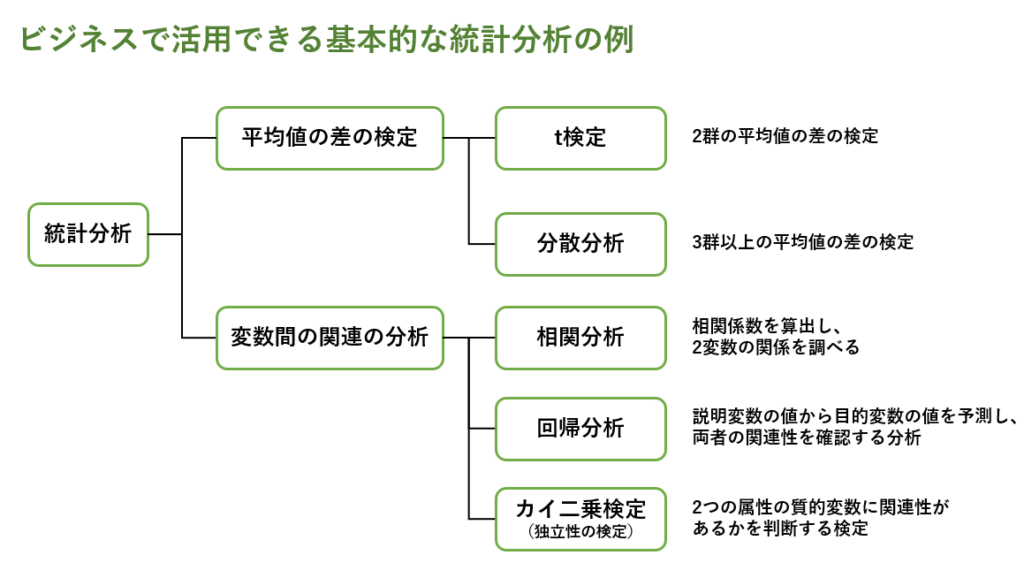
ここからは、それぞれの分析の活用場面と、概要について簡単に説明していきます。
それぞれの分析を解説した記事もありますので、もっと詳しく知りたい方はそれぞれの説明の最後に設置したリンクから確認してみてください。
分析手法① t検定
t検定の活用場面と概要についてご紹介します。
ビジネスにおけるt検定の活用場面
t検定は、以下のような場面で活用できます。
- 顧客から取得したアンケート結果を分析してマーケティングに生かしたい
- 開発した薬の効果を検証したい
- クーポン配信前と配信後での購入数の差が有意なものか知りたい
- 社員の属性(たとえば男性、女性など)によって年収に差があるか知りたい
- 喫煙者、非喫煙者での血圧の差を調べて新サービスの開発やマーケティングに生かしたい
t検定の概要
t検定は、2つのグループの平均に有意な差があるかどうかを判断する分析手法です。
t検定は、大きく分けると以下の3つの種類があります。
- 対応がある場合のt検定
- 分散が等しい場合のt検定
- 分散が異なる場合のt検定(Welch法)
これらは、「対応のあるなし」「母分散が等しいか等しくないか」で使い分けます。
それぞれのt検定の使い分け方や具体的な分析手順、Excelを使った分析の事例など、詳しく学びたい方は以下の記事をご確認ください。
分析手法② 分散分析
分散分析の活用場面と概要についてご紹介します。
ビジネスにおける分散分析の活用場面
分散分析は以下のような場面で活用できます。
- 開発した薬の効果を検証したい
- 支店ごとの営業社員の売上(東京支店、大阪支店、名古屋支店)に差があるか知りたい
- 研修A受講、研修B受講、研修受講なしの3つのグループで、コンプライアンス意識の高さを比較したい
- とある病気の患者に対して「投薬前」「投薬後1時間」「投薬後2時間」で血圧の変化を知りたい
分散分析の概要
分散分析は、3グループ以上の平均を比較し、有意差があるかを判断する分析手法のことです。
先ほどt検定について簡単に説明しましたが、t検定は3グループ以上では使えないため、3グループ以上の平均値の差の検定を行いたい場合には分散分析を使います。
分散分析は、以下のような種類のものがあります。
- 一元配置分散分析
- 多元配置分散分析
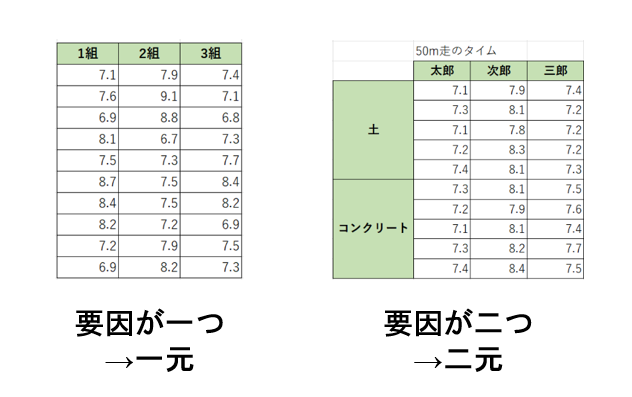
一元、多元というのはデータがもつ「要因」の数です。
たとえば、「職業別」「年齢別」のように要因が二つある場合は「二元」といいます。
この要因の数に応じて使う分散分析の種類も変わってくるということですね。
分散分析の概要や、一元配置分散分析の手法、具体的な分析事例について詳しく学びたい方は、以下の記事をご確認ください。
分析手法③ 相関分析
相関分析の活用場面と概要についてご紹介します。
ビジネスにおける相関分析の活用場面
相関分析は、以下のような場面で活用できます。
- ECサイトのレコメンドを最適なものにしたい
- 天気と特定の商品の売上の関連性を知りたい
- マーケティングにかけた費用と売上の関連をみたい
- 入社時試験の成績と、入社後の成績との関連をみたい
相関分析の概要
相関分析は、2つのデータに関係性があるか明らかにする分析手法です。
相関の強さを、相関係数という「-1~1」までを取る値で表現します。
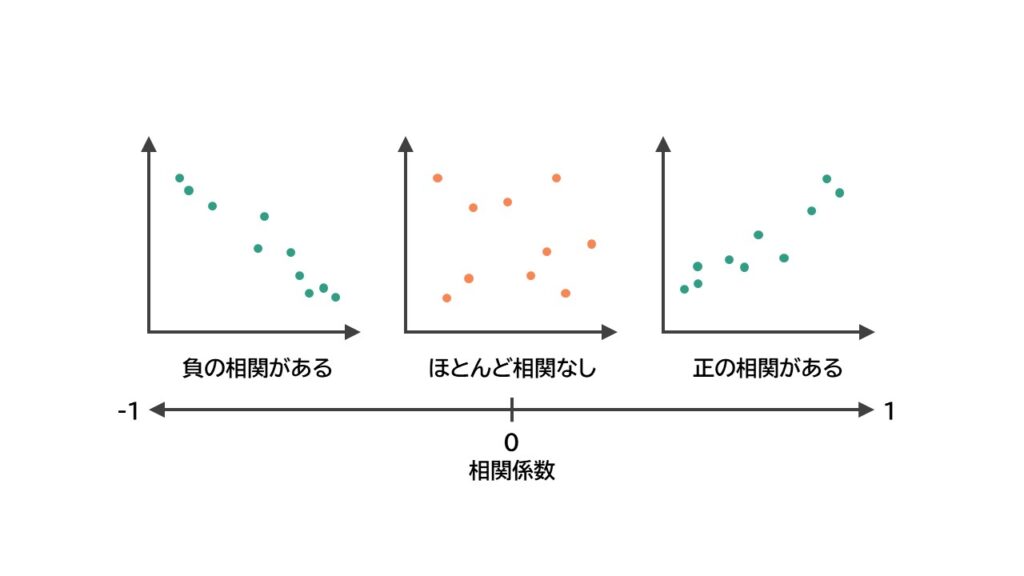
-1に近いほど負の相関があり、1に近いほど正の相関があるというふうに考えることが出来ます。
- 正の相関・・・2変数間において、一方が増加すると、もう一方も増加するような関係。(たとえば年功序列制の会社では、年齢と年収で正の相関がみられることがあります)
- 負の相関・・・ 2変数間において、一方が増加すると、もう一方は減少するような関係。(たとえば、 気温が下がると、カイロの売上が上がるというのも負の相関の例)
ただし、「相関関係がある」=「因果関係がある」というわけではないという点には注意が必要です。
相関分析の手順や注意点、相関係数の読み取り方、Excelを使った分析方法など詳しく学びたい方は、以下の記事をご確認ください。
分析手法④ 回帰分析
回帰分析の活用場面と概要についてご紹介します。
ビジネスにおける回帰分析の活用場面
回帰分析は、以下のような場面で活用できます。
- 生活習慣病とその原因( 年齢、性別、身長、体重、BMI、喫煙歴、飲酒習慣、運動習慣など )について調べ、新薬の開発やマーケティングに活用したい
- 店舗の一日の売上をさまざまな要因( 最寄り駅からの距離、駐車可能台数、店舗の面積、商品数、レジの平均待ち時間、一日当たりの来店数、一日当たりの売上、地域の住人数など )から予測し、経営戦略に役立てたい
- 従業員のエンゲージメントについて、さまざまなデータ(アンケートの回答や年収、残業時間、年齢)などから、影響を大きく与えている要因を探り、社内環境の改善につなげたい
回帰分析の概要
回帰分析は、説明変数と目的変数の定量的な関係を調べる分析手法です。
分析した結果をもとに、将来の予測に活用していくことができます。
基本的な回帰分析としては、説明変数が一つの単回帰分析と、説明変数が複数の重回帰分析があります。
重回帰分析を使うと、複数の変数を同時に分析でき変数間の相関関係を調べることができます。
Excelを使った回帰分析の具体的な手順や、出力結果の読み取り方などについて詳しく学びたい方は、以下の記事をご確認ください。
回帰分析とは 特徴やExcelでの分析方法を分かりやすく解説
分析手法⑤ カイ二乗検定(独立性の検定)
カイ二乗検定の活用場面と概要についてご紹介します。
ビジネスにおけるカイ二乗検定の活用場面
カイ二乗検定は、以下のような場面で活用できます。
- アンケート結果のなかの2つの属性に関連性があるかどうかを知りたい
- ある薬剤を投与したグループと投与していないグループで、血液検査の正常異常の割合が有意なものか確かめたい
- バナーAとBの広告のクリック率の差が有意なものか調べたい
- Aという勉強法を使った学生と、Bという学習法を使った学生の合格率の差が有意なのか確かめたい
カイ二乗検定の概要
カイ二乗検定は、 カイ二乗分布を利用した統計的検定の総称です。
なかでも代表的なカイ二乗検定の手法として「独立性の検定」という2変数間に関連があるのかどうかを検定する手法があります。
具体的には「期待値」と実際の「観測値」のずれが誤差といえるのか、確率的にそうそうあり得ないほどのずれなのかなどを調べ、差の有意性を判断する分析です。
t検定と似ているように思えますが、t検定は2グループの平均値の差を見る検定であるのに対し、カイ二乗検定は 2グループの割合の差を見る検定であるという違いがあります。
独立性の検定とは 概要や検定の手順、ビジネスにおける活用場面をご紹介
まとめ
今回は、ビジネスで役に立つ基本的な統計分析の手法をご紹介しました。
基本的なものとはいえ、統計学をあまり知らない方からすると目新しい分析手法もあったのではないでしょうか。
これらの分析手法を扱えるようになるだけでも、日々何気なく接していたデータの見え方が変わってくるかもしれません。
是非今回ご紹介した分析手法をもとに、社内で眠っている数々のデータを分析し、課題解決へとつなげてみてください。
\ この記事を読んだ方におすすめ! /






-520x312.png)