回帰分析とは 特徴やExcelでの分析方法を分かりやすく解説
目次
回帰分析とは
回帰分析は、原因から結果を予測するときによく使われる分析方法です。
説明変数が目的変数とどのような定量的な関係があるのかを調べ、それを明らかにしたうえで将来の予測に活用していきます。
回帰分析は統計学を勉強しないと少しなじみがない分析方法ですが、Excelを使うことで簡単に分析ができるので、是非この機会に覚えてみましょう。
回帰分析の種類
回帰分析には、単回帰分析と重回帰分析の2種類があります。
まずはそれぞれの違いについて説明します。
単回帰分析
単回帰分析は、原因とみられる1つの要素から、ある結果を予測するための手法です。説明変数が一つ（単一）なので単回帰分析とよばれています。
単回帰分析では、結果を予測するとき「y=ax+b」という直線の式を用いて表します。
このxの部分が説明変数となり、yの部分が目的変数を表します。
重回帰分析
重回帰分析は、説明変数が複数存在している場面において、結果を予測する際に用いる分析手法です。
要は、単回帰分析よりも説明変数が多い場合に使う、というイメージを持っていただければと思います。分析手法の根本的な考え方としては、単回帰分析と変わりありません。
予測する際の直線の式としては、以下の通りです。
説明変数が増えたので、a₁x₁、a₂x₂などのように複数のxが出てきています。
回帰分析の仕組み
回帰分析では、回帰直線という直線の式を求めていきます。この回帰直線は「最小二乗法」という方法で求めていきます。
最小二乗法は、一言でいうと「残差の二乗和が最小になるようなもっとも当てはまりのいい回帰直線を求める方法」です。
最小二乗法については、以下の記事で詳しく説明していますので、是非合わせてご確認ください。
回帰分析のメリット
まず、回帰分析を行うメリットについてご紹介します。
統計学に基づいた根拠ある分析結果や予測が得られる
回帰分析を行うことで、統計学に基づいた根拠ある分析結果や予測が得られるという点がメリットとしてあげられます。
回帰式が得られれば、式に数字を当てはめるだけで統計学に基づいた予測が出来るので、ビジネスにおいては売上予測、販売数予測など様々な場面で役立ちます。
感覚ではなく、過去のデータに基づいた予測を立てることで、「不良在庫を減らす」、「適切な人員配置ができる」などにより利益の改善につなげることもできます。ビジネスマンの方には是非覚えていただきたい分析手法の一つです。
回帰分析の注意点
回帰分析は非常に便利な分析手法ですが、いくつか注意点があります。
多重共線性
説明変数が複数である「重回帰分析」を実行する際の注意点として「多重共線性」というものに気をつける必要があります。
多重共線性とは、相関係数が0.9を超えるようなかなり強い相関がみられる変数を一緒に説明変数に加えることで、分析結果が不安定になり正しい結果が得られないということを指します。
多重共線性が生じないように、事前に変数間の相関を確認しておくことが大切です。
もしかなり相関が強い変数が見られた場合の対応としては、「一方の変数を取り除いて分析を実施する」か、「2つの変数をあわせて1つの変数にする」などで対応するのがよいでしょう。
説明変数の数は多すぎてもよくない
重回帰分析を行うときに説明変数の数が多すぎると正確な分析結果が出なくなってしまう可能性があります。
目安としては「説明変数はデータの総数の1/15まで」と覚えておくとよいでしょう。
説明変数が多すぎる場合の対応としては、「データの総数を増やす」か「説明変数を減らして分析する」などがあります。
「予測」と「現実」は異なる場合がある
回帰分析で求めた回帰式に当てはめて将来の予測をすることは出来ますが、あくまでも「予測」にすぎません。
そのため、求めた直線の式を使って予測したものの、現実の結果が大きく異なるということもあります。
たとえば、回帰分析の結果、1日に商品が100個売れると予測したものの、たまたまＳＮＳで取り上げられて、突発的に売上が増加して予測結果と大きく異なってしまったといったケースも考えられます。
そのため、あくまでも予測の1つの判断材料として活用するようにし、イレギュラーな事象がある場合には、これまでの経験をもとに臨機応変に対応していくといったことができるようにすることも大切です。
また、単回帰だと予測が不十分な場合には、重回帰分析にして説明変数を追加するなどを行い、より現実に即した予測が出来るように分析ができるよう改善するといったことも重要です。
Excelを使った回帰分析の方法
ここからはExcelを使った回帰分析の方法についてご紹介します。
「データ分析」アドインの追加
前提として、Excel上で回帰分析を行うためには「データ分析」ツールをアドインで追加する必要があります
データ分析ツールの準備の流れは以下の通りです。
「ファイル」
→「オプション」
→「アドイン」
→「設定」とクリックしていきます。
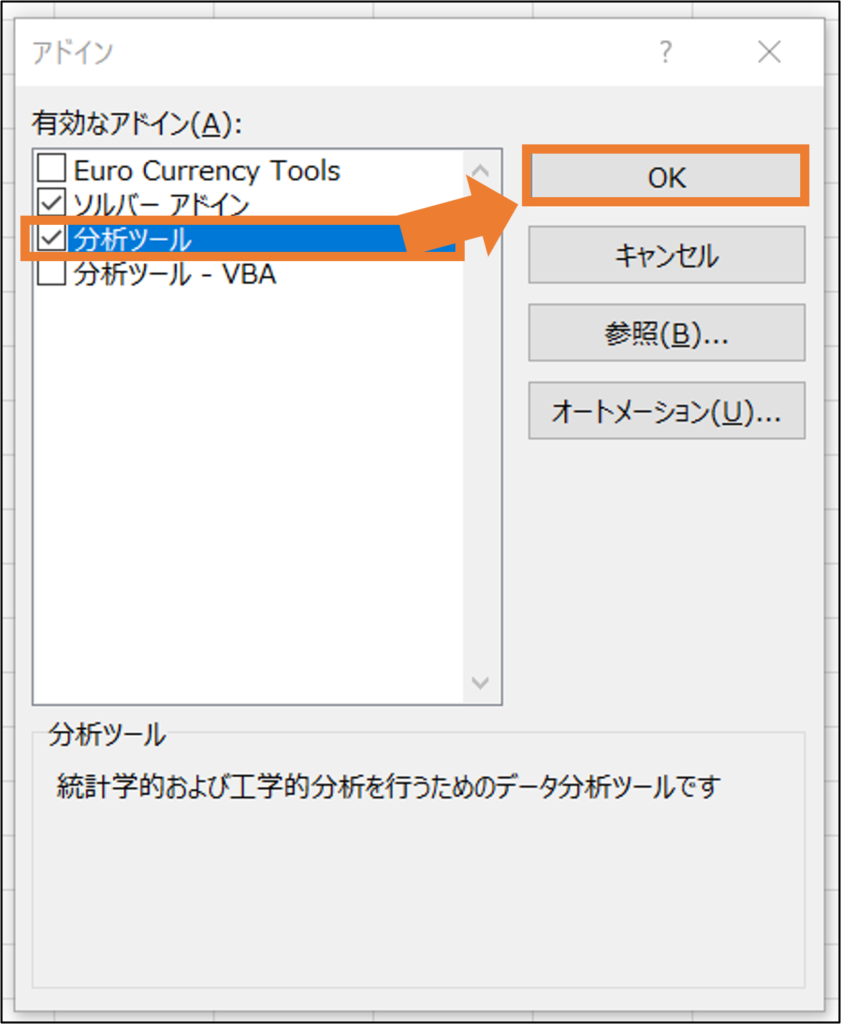
ここで出てきた「分析ツール」にチェックを入れOKをクリックします。
データ分析ツールの準備が完了です。
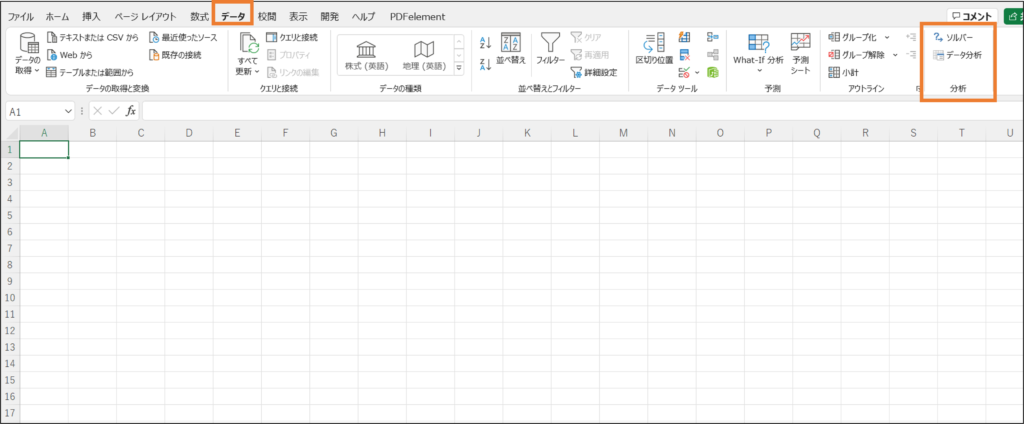
もしデータアドインを入れていなければ、上記の手順で設定したうえで進んでください。
回帰分析の手順
回帰分析は、以下の手順で進めていきます。
- データの準備
- データ分析の実行
- 出力結果の読み取り
① データの準備
まずは定量データを用意します。
説明変数と目的変数がいるので最低2列以上用意しましょう。
今回は以下のようなデータを用意しています。
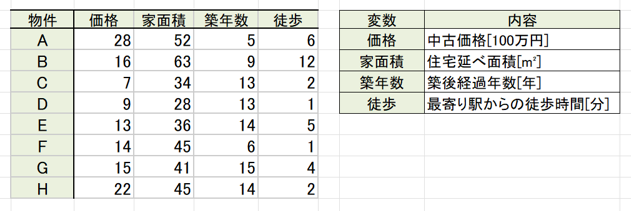
中古物件の価格を家面積、築年数、最寄り駅からの徒歩時間などの変数から回帰分析していきます。
② データ分析の実行
まず、以下の手順で進めていきます。
「データ」
→「データ分析」
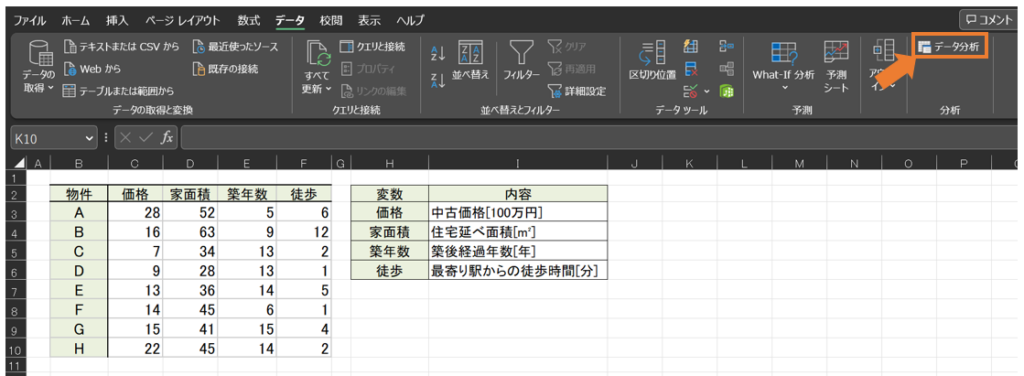
「回帰分析」を選択し、OKをクリックします。
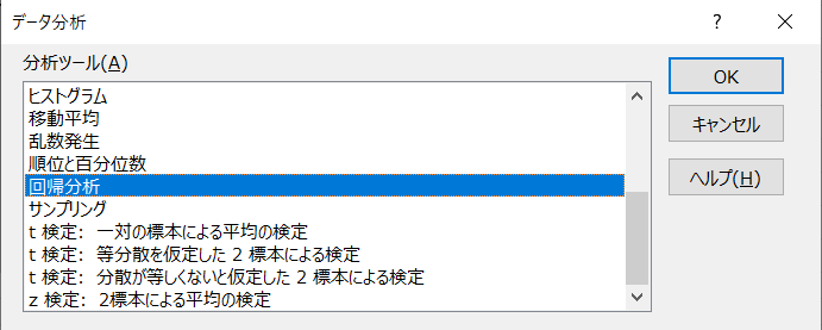
そして、目的変数と説明変数の範囲をそれぞれ指定します。
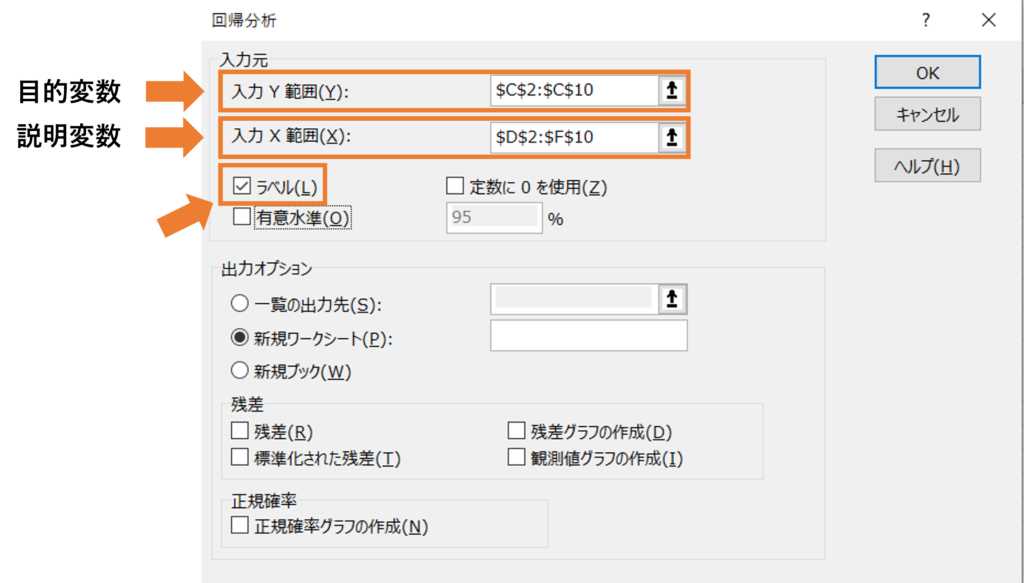
最後に、ラベルにチェックを付けOKをクリックすると、以下のような分析結果が出力されます。
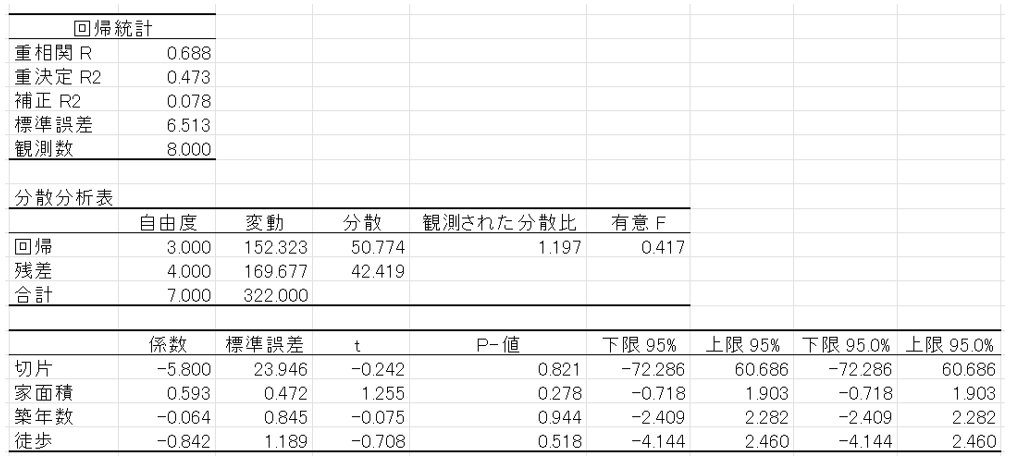
③ 出力結果の読みとり
出力結果には様々なデータが記載されていますが、基本的な確認すべきポイントは「回帰式」「決定係数」「p値」の３つです。
回帰式を確認
回帰式というのは、いわゆるy=ax+bといった式のことです。
出力結果では回帰式はそのまま出てきませんが、出力された情報に回帰係数と切片があるため回帰式を把握することが可能です。
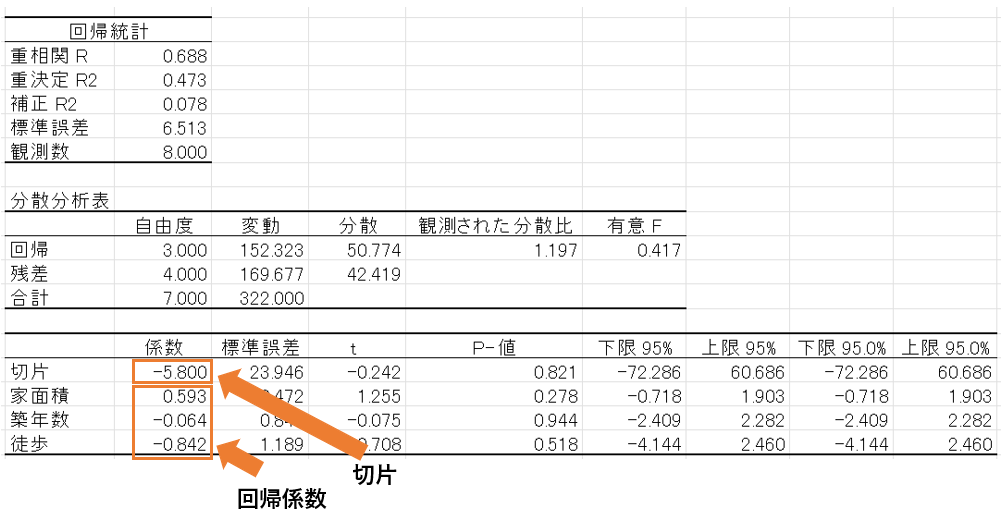
今回の場合、回帰式は「y=0.593x₁＋（-0.064）x₂＋（-0.842）x₃ – 5.800 」となります。
もっと分かりやすくすると、
「中古価格＝ 0.593 × 家面積 ＋
（-0.064）× 築年数 ＋
（-0.842) × 徒歩 ＋
（- 5.800 ）」
ということですね。
回帰式より、家面積が広くなるほど価格が高くなることや、築年数が古いほど価格が落ちることなどが分かります。
また、今後新しい中古物件が出てきたとき、回帰式に具体的な家面積や築年数、徒歩時間などの数値を当てはめることで、価格の予測（参考にすること）が可能です。
決定係数で当てはまりを評価
決定係数は0～1の値を取り、1に近いほど回帰直線の当てはまりが良いことを示す指標です。
当てはまりの良さとは、予測精度の高さのようなイメージを持っていただければと思います。
明確な判断基準はありませんが、0.5を超えると当てはまりが良いと判断する場合が多いです。
その理由は、決定係数は相関係数を2乗した値だからです。
一般的に相関係数0.7あれば相関があるといえることが多いため、その2乗である0.49（≒0.5）が一つの判断基準になるということです。
出力結果で、決定係数にあたる部分は「重決定 R2」の部分です。
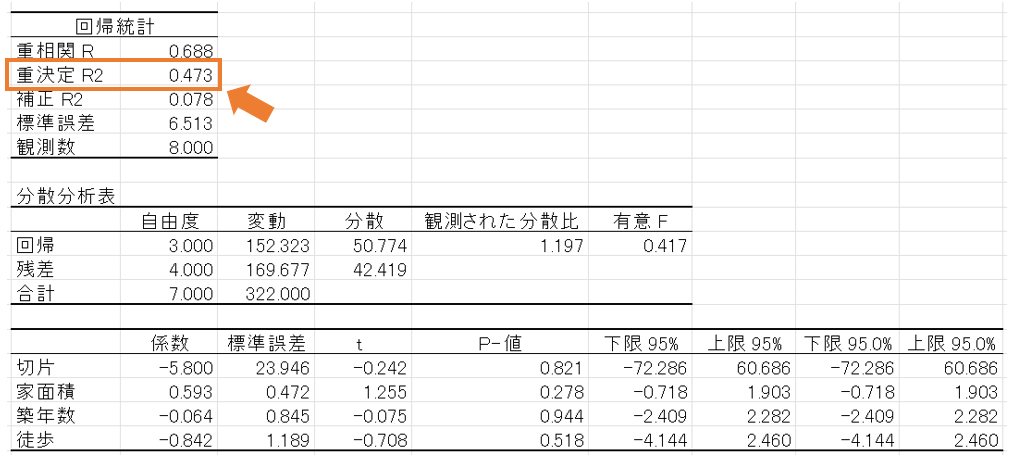
今回は決定係数が0.473ということなので、回帰式の予測精度はそれほど高いとはいえません。
回帰式で将来の予測を行い、決定係数で予測精度を確認するというイメージです。
p値で有意性を確認
p値は、帰無仮説（ 回帰係数＝０）が支持される確率です。
そのため、p値が極端に小さい場合（一般的には0.05を基準に下回った場合）、回帰係数が0である可能性が低いことになります。
回帰係数が0でないことは、その説明変数が目的変数に対し影響を与える因子であることを意味します。
出力結果で、p値にあたる部分は以下の部分です。
今回、p値が0.05を下回っている説明変数がありません。
つまり、今回の分析結果では、統計的に説明変数に意味がなかったということを示しています。
ただし、注意点として認識しておいていただきたいのは、もし有意差が見られたとしても関係性はまた別の話だということです。
p値で有意差ありという結果になったとしても、データ量などによってもその分析結果が使えるものなのかどうかも変わってきます。
そのため実際の関係性については、データを見て判断することが重要です。
ビジネスにおける回帰分析の活用事例
さて、ここからはビジネスにおける回帰分析の活用例についてご紹介します。
ケース1 疾病の要因調査
例えば、とある生活習慣病とその原因についての調査があります。
年齢、性別、身長、体重、BMI、喫煙歴、飲酒習慣、運動習慣など、様々な事柄を要因と仮定し重回帰分析を行います。
そうすると、どういった特徴や習慣が生活習慣病の発症にどの程度影響しているのかを推定することができます。
そこで、その習慣を改善するためのサービスや商品（ex.薬、運動器具など）を提供することで、ビジネスにつなげることができます。
ケース2 コンビニの新店舗の売上を予測
コンビニやスーパーなどの店舗の売上予測にも回帰分析は有効です。
たとえば、既存の系列店舗のデータから、新店舗の売り上げを予測することができます。
データとしては、最寄り駅からの距離、駐車可能台数、店舗の面積、商品数、レジの平均待ち時間、一日当たりの来店数、一日当たりの売上、地域の住人数など、売上を予測するための様々な変数があります。
これらの情報をもとに、回帰直線を求めることで、新店舗の売上を予測することが可能です。
ケース3 マンション販売価格相場の予測
さきほどのExcelでの分析例のように、「家面積・築年数・距離」などをもとに価格の予測をすることができます。
周辺地域にある不動産から説明変数とするデータを収集してきて、回帰分析を行うことで、高すぎず安すぎない、適切な価格を設定することができます。
ケース4 気温により、カフェのアイスコーヒーの売上個数を予測する
たとえば、説明変数xを気温、目的変数yをアイスコーヒーの売上個数とし、過去のデータをもとに回帰分析を行うことで、気温による販売予測が可能になります。
たとえば、分析の結果「y = 11.3x – 7.65」という式が得られたとします。
そうすると、気温が30℃のときには、「y = 11.3×30– 7.65=331.35個」、気温20℃の時には「y = 11.3×20– 7.65=218.35個」というふうに計算でき、おおよその売上個数の予測ができます。
このように過去のデータに基づいて予測をすることで、無駄に在庫を抱えるリスクや、廃棄処分を減らすことにつながります。
出力結果の用語解説
最後に、回帰分析の出力結果について、簡単に用語を解説していきます。
| 重相関 R | 決定係数の正の平方根。1に近いほどよく近似されたモデルであることを示す。 |
| 重決定 R2 | 0～1の値をとる回帰分析の当てはまり度合いを表す指標。1に近いほど当てはまりがよい。 |
| 補正 R2 | 自由度を考慮した回帰分析の当てはまり度合いを表す指標。 1に近いほど当てはまりがよい。 |
| 標準誤差 | 目的変数の推定値と観測値のばらつきの度合い。大きいほど精度が悪い。 |
| 観測数 | データの数 |
| 残差 | 観測値から予測値を引いた結果 |
| 自由度 | グループ間の自由度 |
| 変動 | グループ間の平方和 |
| 分散 | 変動を自由度で割った値。この値が大きいほどデータのばらつきが大きい。 |
| 観測された分散比 | グループ間の分散を残差の分散で割ったもの |
| 有意F | 「切片以外の全ての説明変数は無効（係数は0）」という帰無仮説のもと、偶然の誤差の影響により標本の関係が観測されてしまう確率の上限のこと。ゼロに近いほど、偶然の結果である可能性が低く、意味のある回帰式を得られたことを示す。 |
| 係数 | 重回帰式における係数 |
| t | 推定係数を標準誤差で割った値。tの絶対値が大きいほど影響度合いが大きい。 |
| P-値 | 観測された分散比をもとに行った検定結果で、帰無仮説が支持される確率。一般的にはp値が0.05以下の時、帰無仮説を棄却し、対立仮説を支持することが多い。 |
| 下限95%・ 上限95% | 信頼係数95%のとき、真の係数があると思われる範囲 |
まとめ
回帰分析を上手く使いこなすことができれば、課題の発見や、効率よく売上を伸ばす施策を検討する際に役立ちます。
ただし注意点として、回帰分析で導き出した直線の式（傾きや切片）はあくまでも傾向を表しているだけであり、絶対的なものではないということは忘れないでください。
回帰分析を活用して、正しい予測でビジネスを加速させていきましょう。
＼ この記事を読んだ方におすすめ！ ／
