今回は、アンケート結果の分析に役立つ独立性の検定についてご紹介していきます。

＼ この記事を読んだ人がよくダウンロードしている資料（無料） ／

独立性の検定とは

独立性の検定とは、「カイ二乗検定」の一種です。

カイ二乗検定というのは、カイ二乗分布と呼ばれる確率分布に基づいた検定全般を指します。

カイ二乗検定には、「独立性の検定」や「適合度の検定」などさまざまな検定がありますが、なかでも代表的なカイ二乗検定として「独立性の検定」があげられることも多いです。

独立性の検定とは、簡単にいうと2つの質的データが関連しているのか、独立しているのかを検証するための統計的検定です。

よく独立性の検定が使われる場面としては、アンケート結果の分析があります。

例えば、ラーメンの味と性別でアンケート調査を行ったとします。

そのとき２つの変数が独立している場合、性別と好きなラーメンの味と関連がないということになります。

逆に独立しているといえない場合は、性別が好きなラーメンの味と関連があるということがいえます。

もし関連がある場合には、公式LINEやメルマガなどから発信するラーメンの情報を性別ごとに変えてみたりすることで、マーケティングの効果を高めることもできます。

このように、2つの質的データが関連しているのか、独立しているのかを確かめることは、ビジネスに役立つ検証だといえます。

独立性の検定を使うための条件

独立性の検定を使う際には、以下の2つの条件が必要になります。

• 期待値が1以下のデータが存在しない
• 期待値が5以下のデータが表の中に2割以上存在しない

クロス集計における期待値というのは、変数間が独立であった場合に合計の比率から逆算して求められる度数のことです。（期待度数ともいいます）

もし、この条件を満たしていないが独立性の検定を行いたいという場合には、いくつかのデータをカテゴリでまとめて条件を満たすようにしたうえで利用するようにしましょう。

独立性検定の手順

独立性検定の分析手順は以下の通りです。

1. 事前準備
2. 検定の実施
3. 結果の解析

それぞれの手順について解説します。今回は「映画館で観る映画のジャンルとポップコーン購入の関係性」を例に解説していきます。

ちなみに、これから紹介する分析手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。

事前準備

実際に検定に入る前に、事前準備から始めていきます。

目的の明確化

まずは、何の関係性を検証したいのかを明確にすることが大切です。

なぜなら目的が明確になっていないと、分析に必要なデータが集められていなかったということにつながりかねないからです。

今回でいうと「とある映画館における映画のジャンルとポップコーン購入の関係」という目的があります。

まずは目的を明確にして、その分析に必要となるデータを集めるようにしましょう。

データ確認

目的が明確になったら、データを収集（すでにデータがある場合は確認）します。

今回は、とある映画館に訪れた600人を対象に、1人1人が見た映画のジャンルとポップコーン購入の有無を調査したという架空のデータをもとに検定の手順を確認していきます。

今回使う調査結果は以下の表の通りです。

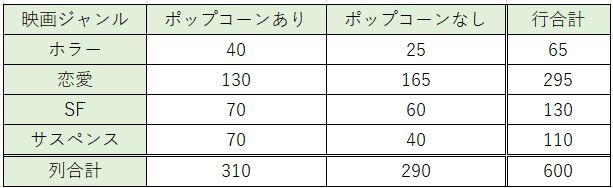
条件を満たしているかの確認

さて、まずは独立性の検定を行う際に必要な条件を満たしているかもしっかり確認するようにしましょう。

ジャンルとポップコーンの数値が上記表の場合、期待値は行と列の合計に基づいて以下のように計算できます。

「行合計×列合計÷総合計」

たとえば、ホラー/ポップコーンありの場合は以下のように計算できます。（小数点は四捨五入しています。）

「　65（ホラーの行合計）×310（ポップコーンありの列合計）÷600（総合計）=34　」

これと同じ全てのセルで計算すると、期待値は以下の表のようになります。

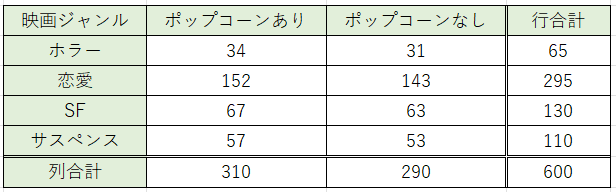
これで期待値を全て求めることができました。

また、期待値が独立性の検定を行う際に必要な以下の条件を満たしていることも分かるため、検定を進めるうえで問題ないこともわかります。

• 期待値が1以下のデータが存在しない
• 期待値が5以下のデータが表の中に2割以上存在しない

有意水準の設定

続いて、有意水準を設定していきます。

有意水準というのは、統計的検定において帰無仮説（否定したい仮説）を棄却する（間違っていると判断することができる）基準のことです。

たとえば、「映画のジャンルとポップコーンのありなしは独立している」という帰無仮説が間違っていると判断することが出来れば、「映画のジャンルとポップコーンのありなしは関連している」ということがいえます。

多くの場合、有意水準は5%で設定しますので、ここでも5％で考えていきます。

ただし、絶対に5%でなければならないことはありません。

もし基準を厳しく設定したい場合は1％にするなど、検定の目的に応じて使い分けるということも覚えておきましょう。

仮説の設定

検定では、帰無仮説を立てて、その帰無仮説を棄却できるかどうかで結果の読み取りを行っていきます。

※帰無仮説というのは「否定したい仮説」のことです。

独立性の検定では、基本的に2つの質的データが独立であるという帰無仮説を立てます。

今回の場合では、「映画のジャンルとポップコーンのありなしは独立している」という帰無仮説を立てます。

この仮説を棄却（否定）することができれば、２つの質的データは独立していない、つまり関連があるというふうに考えることができます。

検定の実施

検定で計算する手順は以下の通りです。

1. 「検定統計量」を求める
   計算方法：各セルで、『(実測値-期待値 )²÷期待値 』を求める
   求めた値を足し合わせる。
2. 検定統計量とカイ二乗値を比較する

「(実測値-期待値 )²÷期待値 」をわかりやすくするために細かく分けて説明していきます。

まずは、「実測値-期待値 」を求めます。すると、以下のようになります。

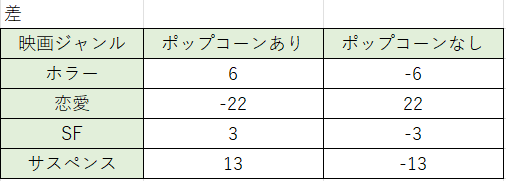
求めた値を二乗し、二乗差を求めていきます。

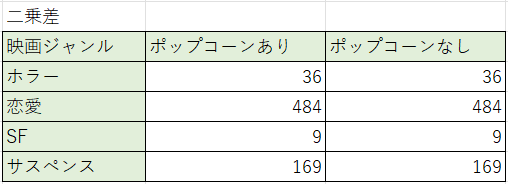
二乗差を求めたら、それぞれ期待値で割っていきます。

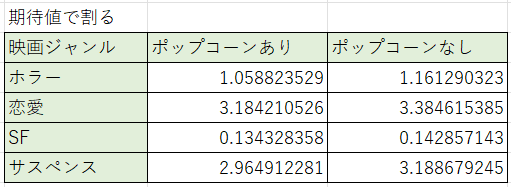
最後に、求めた値を足し合わせていきます。

そうすると、以下の通りになりました。こちらが検定統計量です。

結果の読み取り

自由度は、（行数―1）×（列数―1）で求めることが出来ます。

つまり、今回は行が4行、列が2行のため、自由度は以下のように計算できます。

「　（4－1）×（2－1）＝3　」

つまり、今回の場合自由度は3となります。

これで、あとは有意水準5％、自由度3のカイ二乗値を調べれば、必要な数値はそろいます。

あとは、以下のカイ二乗分布表から該当箇所を読み取っていきます。

カイ二乗分布表は、横軸に確率p、縦軸に自由度nを取り、行と列の交差するセルに対応するカイ二乗値が記載された表です。

この表では、カイ二乗値がとある値よりも大きくなる確率（上側確率）を表しています。

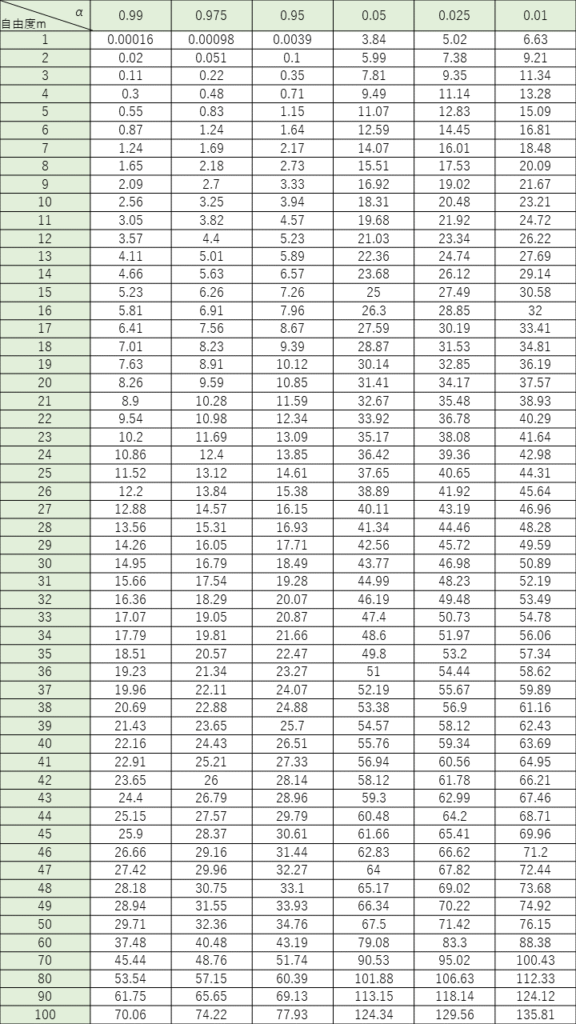
カイ二乗分布表で有意水準5％（0.05）の列、自由度3の行を確認し、カイ二乗値は7.81ということがわかります。

今回の検定統計量15.2は、カイ二乗値7.815を上回っているため、棄却域に入ります。

つまり、「映画のジャンルとポップコーンのありなしは独立している」という帰無仮説を棄却することができ、２つのデータには何らかの関連があるということがいえます。

関連があることが分かれば、上映する映画ジャンルにあわせてポップコーンの在庫を調整するという施策につなげていくことができます。

ビジネスにおける活用場面

独立性の検定はさまざまなビジネスの現場でも活用できる分析です。

たとえば、以下のような活用例もあります。

• スーパーの異なる4か所に同一商品を置いた際の購入有無で検定を行い、設置場所と購入されやすさの関連性を確認する。
• カフェで期間限定のスイーツを販売をした際に、性別や年齢と購入の有無に関係があるか検定することでどのセグメントでアプローチすべきか考えることができる。
• 病気の患者に対して、薬を投与し治療する方法と生活をコントロールし治療する方法を試した際に、病気が改善された人と改善されなかった人で関係性を調べる
• 生活習慣病の罹患有無と朝食の有無の関係性から、朝食と生活習慣病の関係性を調べる。

このようにさまざまな場面で独立性の検定は活用することができます。

是非ご自身の仕事のなかで生かせないか考えてみてください。

まとめ

今回は、独立性検定の概要、検定手順、ビジネスでの活用事例について詳しく解説しました。

独立性検定を正しく活用できるようになれば、社内に眠っているアンケート結果のデータなどから新たな気づきが生まれるかもしれません。

是非この機会に正しく使えるよう覚えておきましょう！

＼ この記事を読んだ方におすすめ！ ／