データ分析に取り組む際には、データの傾向を正しく掴むことが重要です。そして、データの傾向を掴むためによく使われるのが、データの傾向を特定の値で表現する「代表値」という考え方です。
代表値として有名な値に平均値がありますが、この記事では平均値と並んでよく用いられる代表値「中央値」について解説していきます。
\ この記事を読んだ人がよくダウンロードしている資料(無料) /

目次
中央値(MADIAN)とは
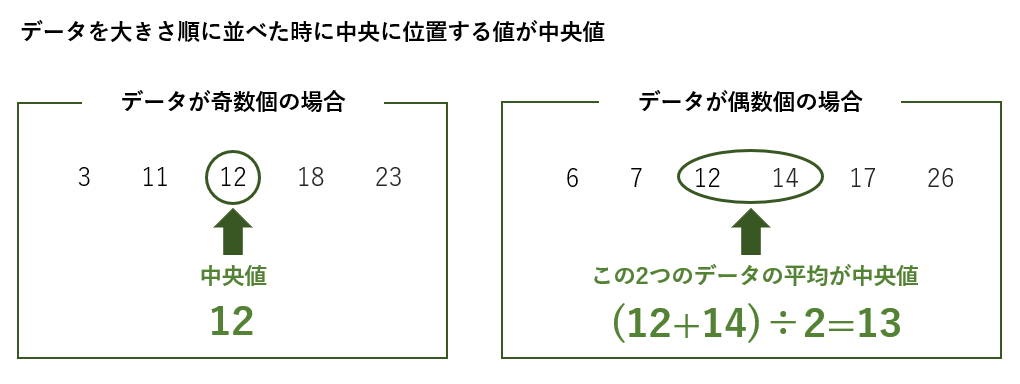
中央値は、データを大きさ順に並べたときに、真ん中にあたる値のことです。
奇数個の場合は、データを大きさ順に並べて真ん中に当たる値がそのまま中央値となり、偶数個の場合は、真ん中に最も近い2つのデータの平均が中央値になります。
ちなみに、真ん中に来る値なので、中央値は別名「50%点」とも呼ばれます。
データの傾向を特定の値で表現する代表値という考え方がありますが、中央値は代表値のうちの一つです。
中央値の求め方(奇数個の場合)
中央値について具体例で考えてみましょう。
以下の身長の男性5人がいるとします。
167cm、175cm、163cm、182cm、172cm
このデータ全体の中央値を考えてみます。
まずは、このデータを小さい順に並び替えていきます。
そうすると、
163cm、167cm、172cm、175cm、182cmという順番になります。
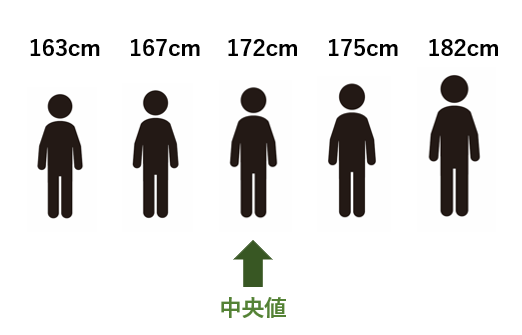
そして、このデータの中で真ん中に位置するデータは172cmです。
そのため、中央値は「172cm」となります。
中央値の求め方(偶数個の場合)
では、167cm、175cm、163cm、182cm、172cm、170cmのように6人のデータ(偶数個)だった場合はどうでしょう。
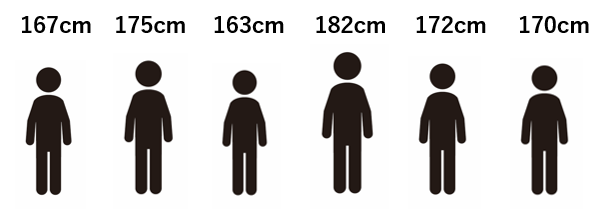
このような場合は、真ん中に最も近い2つの値の平均を中央値とします。
まず、大きさ順に並び替えると以下のようになります。
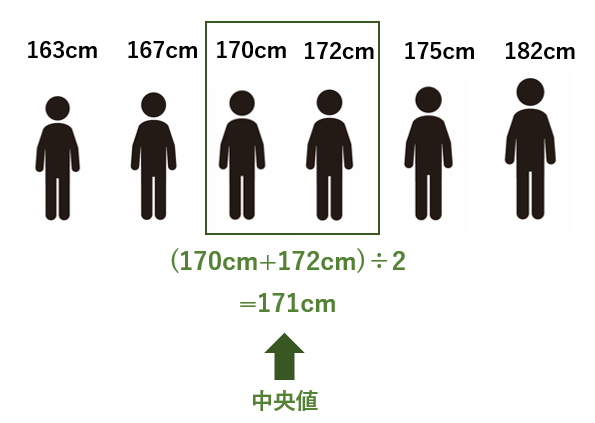
163cm、167cm、170cm、172cm、175cm、182cm
そうすると、真ん中に最も近いデータは170cmと172cmになります。。
よってこの2つのデータの平均を求めれば良いので、(170cm+172cm)÷2=171cmが中央値となります。
中央値のメリット
中央値のメリットは、「外れ値があったときに、その影響を受けにくい」いう点です。
たとえば、167cm、175cm、163cm、172cm、230cmという5人のデータがあったとします。
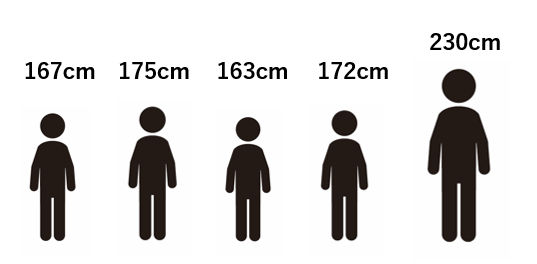
一人だけ飛び抜けて身長が高い人がいますね。
このデータで平均値を求めると181.4cmとなります。実際のデータをみると、167cm~175cmの間にほとんどの人がいるので、この平均値はデータ全体の特徴を分かりやすく表現しているとはいえません。飛び抜けて大きい人の身長に引っ張られて平均値が引き上げられてしまったということですね。
そこで、中央値を考えてみましょう。
奇数個の場合の中央値は大きさ順に並べて真ん中に来るデータなので、172cmが中央値になります。
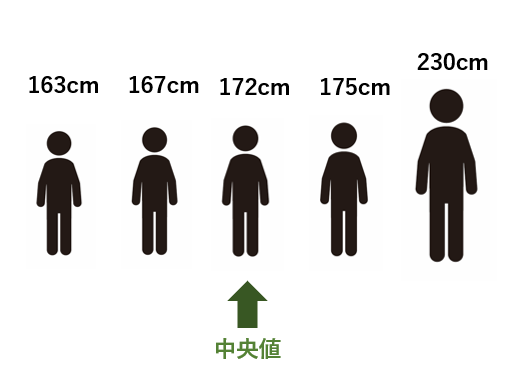
平均値に比べ、172cmという値はデータの特徴を正しく表しているというのが分かると思います。
このように外れ値があったとしても、その影響を受けにくいという中央値のメリットです。
Excelでの中央値の求め方
Excelでは、関数を使えば簡単に中央値を求めることができます。
これから紹介する分析手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。
まず、データを用意します。
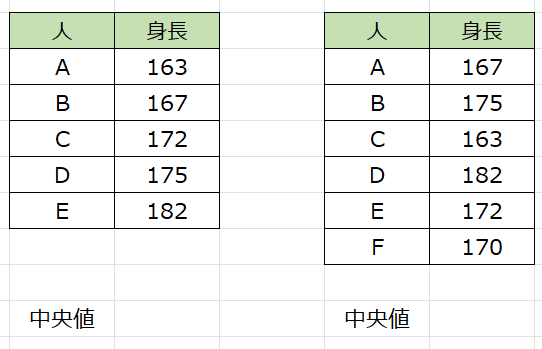
中央値を表示したいセル上に「=MEDIAN」の関数を打ち込み、データの範囲を指定します。
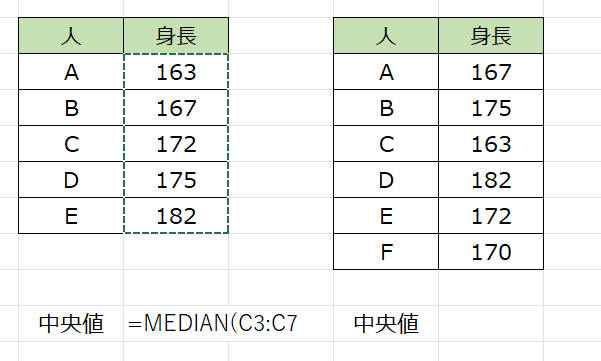
あとは、エンターを押せば中央値が求められます。
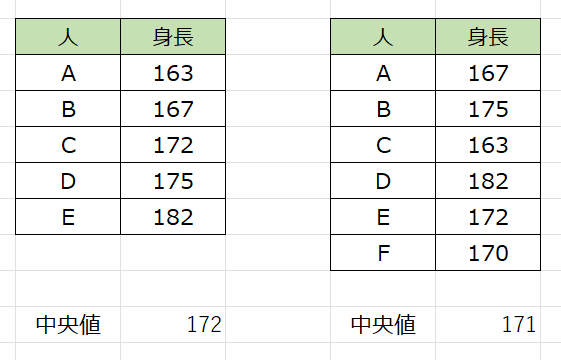
以上が、Excelにおける中央値の求め方です。
中央値を使う際の注意点
中央値は外れ値の影響を受けにくい反面、データ全体の特徴を正確に把握出来ない可能性もあります。
たとえば、先ほどの例で230cmの人がいるというのもデータの一つですが、中央値だけをみていてはそういった外れ値的なデータが存在することなど、データの細かい実態までは把握できません。
そのため、中央値だけでなく様々な指標を確認したり、データ全体を見るなどが重要です。
ビジネスにおける中央値の活用イメージ
ここからは、ビジネスにおいてどういった場面で中央値の考え方が活用出来るのかをご紹介していきます。
事例① 売上の中央値を考える
たとえば、都道府県別で一日あたりの商品販売個数のデータを集計するとしましょう。
その都道府県ごとの平均をとると、一日あたり100個となりました。しかし、実際は購入が集中している首都圏が売り上げのメインの商売でした。そうすると、首都圏のデータに引っ張られて平均が引き上げられてしまっており、中央値を求めると30個となり、平均と大きく乖離していることが分かる、といったこともあります。このように、場合によっては平均よりも中央値を求める方が適切な場合があります。
事例② 平均勤続年数に隠れる実態を知る
とある会社で、社員の平均勤続年数を算出して18年でした。結構長いから安心だと思う経営者の方もおられるかもしれません。しかし、実際の中央値を見てみると9年でした。これより、一部の長く勤続している人に引っ張られているということが考えられます。
そうすると思っているよりも平均勤続年数が短いので、もっと勤続年数が長くなるような仕組みを作ることも重要になってきます。
中央値以外の代表値の紹介
中央値は代表値と呼ばれる値の一つです。ここからは、中央値以外の代表値について簡単にご紹介します。
平均値
平均値は、「データ全体の値の合計÷データの個数」で求める、データ全体の値を平らに均した値のことです。
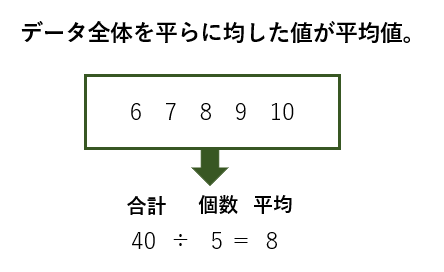
小学校でも習う指標なので、多くの方に馴染みがある言葉だと思います。
平均値については以下の記事で詳しく紹介していますので、是非読んでみてください。
最頻値
最頻値(さいひんち)とは、その名の通り、データのなかで最も頻繁に現れる値のことです。
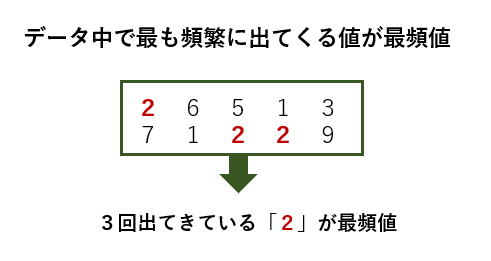
最頻値のメリットは、中央値同様、外れ値に強いという点です。一方、最頻値が複数になる場合があることや、データ数が少ないと使えないというデメリットがあります。
まとめ
一つの指標だけをみて、データの特徴をつかんだ気にならないよう注意が必要です。
たとえば、平均は小学校でも習うので馴染みのある指標ですが、平均ばかりを見ていると、実態とかけ離れていることもあります。逆に、中央値だけを見れば良いということでもありません。
複数の指標をみたり、図などと組み合わせながらデータの特徴を探っていったり、ときにはデータの収集方法や計算方法などの背景まで確認する、といった慎重さが大切になってきます。
\ この記事を読んだ方におすすめ! /