データ分析では、データの傾向を正しく把握することが重要です。そして、データの傾向を掴むためによく使われるのが、データの傾向を特定の値で表現する「代表値」という考え方です。

この記事では最もよく用いられる代表値「平均値」について解説していきます。

＼ この記事を読んだ人がよくダウンロードしている資料（無料） ／

平均（算術平均）とは

平均値は、データ全体の値を平らに均した値のことです。

一般的に知られている「データ全体の値の合計÷データの個数」で求める平均のことを、正確には算術平均といいます。

算術平均の具体例

算術平均について、具体例をもとに考えてみましょう。

たとえば、A社には5人の営業社員がいます。

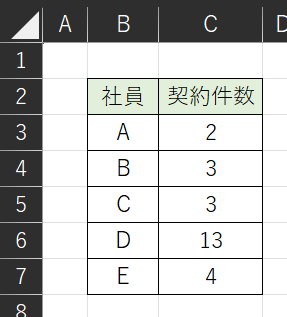
彼らの前月の営業成績（契約件数）が、それぞれ「2件、3件、3件、13件、4件」でした。

このデータをもとに平均値を考えると、営業社員の契約件数の平均は「(2+3+3+13+4)÷5=5件」となります。

データの値を全て足して個数で割るだけなので、シンプルですね。

算術平均のメリット、デメリット

続いて、算術平均のメリット/デメリットをご紹介します。

平均値は、データ全体を対象に求める値です。そのためデータ全体の特徴を把握できるというのがメリットです。

しかし、平均値には外れ値の影響を受けやすいというデメリットもあります。外れ値というのは、簡単にいうと「その他のデータに比べて、極端に大きい、または小さい値」のことだと思ってください。

さきほどの契約件数の例をみると、平均値は5件ですが、実態として5件を超えている社員は13件取った人だけです。その13件という大きなデータに引っ張られて平均値が引き上げられてしまったのです。このように外れ値の影響を受けやすいというのが平均値のデメリットです。

平均値を使ってデータの特徴を把握する際は、実際のデータも確認しながら、外れ値が含まれていないかなど確認して活用することが重要です。

算術平均のExcelでの求め方

それではExcelを使った算術平均の求め方について具体的にみていきましょう。ちなみに、これから紹介する手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。

先ほど例で示したものと同じ、以下のデータで考えます。

5人の社員の平均契約件数を求めていきます。

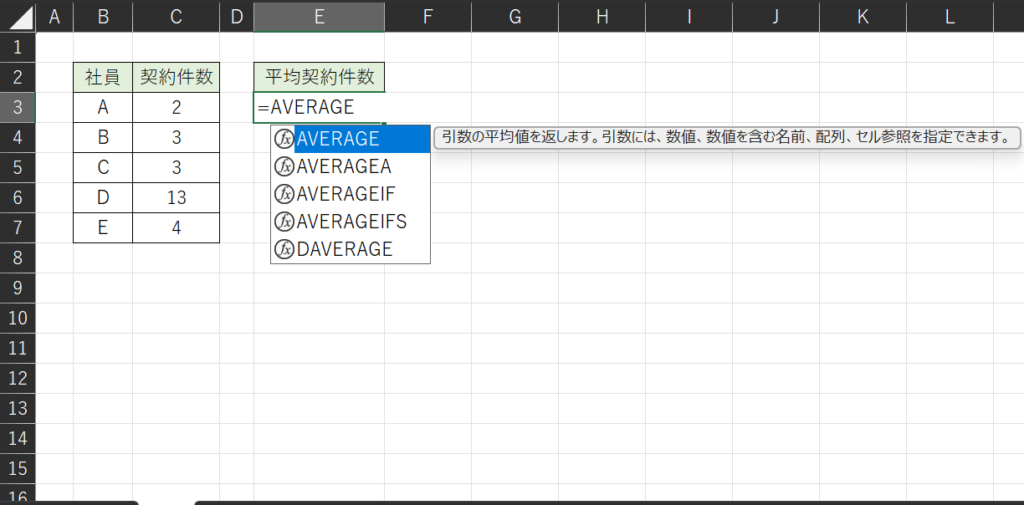
まずは、セルに「=AVERAGE」と入力し、AVERAGE関数を選択します。

セルの範囲選択を使用して、該当のデータ範囲を選択します。

今回の場合、「C3:C7」と入力しています。

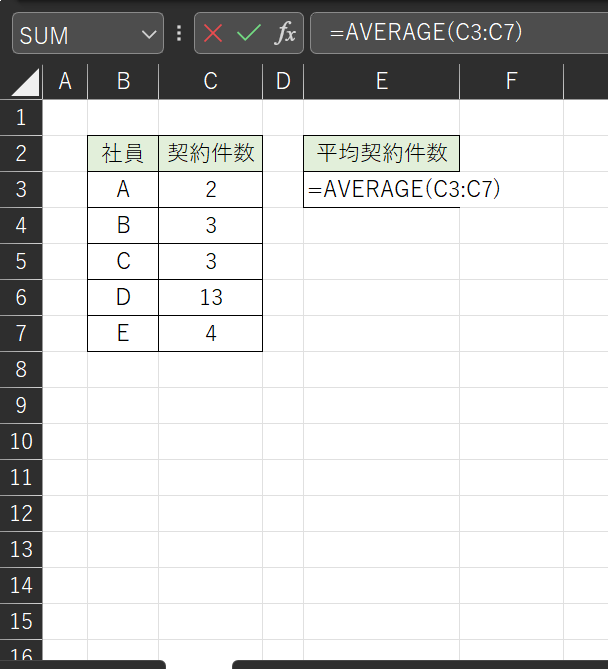
Enterをクリックし、算術平均を求めることができます。

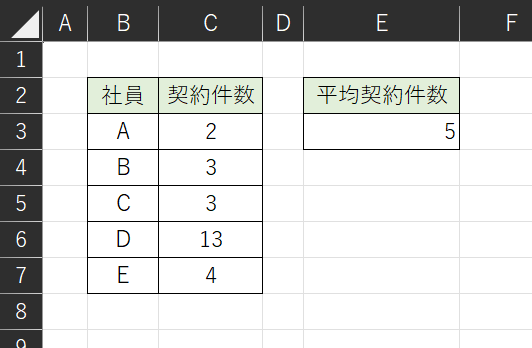
「(2+3+3+13+4)÷5=5件」ということで、ちゃんと5が求められています。

ちなみに、平均はセルに「＝AVERAGE」と入力せずとも、「数式」タブから「オートSUM」⇒「平均」を選ぶことでも簡単に求めることができます。

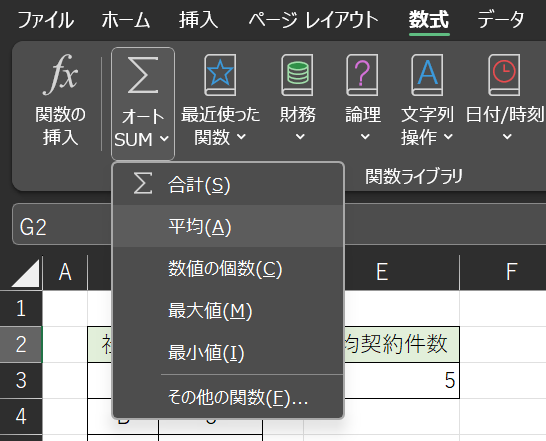
わざわざ関数を入力する手間が省けるので、是非こちらの求め方も覚えておきましょう。

そのほかの主要な平均

平均といえば算術平均のことを指すのが一般的ですが、実は平均にはいろいろな種類があります。

以下で主要な平均について簡単に説明します。

加重平均とは

加重平均は、それぞれのデータの重みを加味して求める平均値のことです。

たとえば、以下のようなカフェの販売データがあったとします。

• ケーキ 　1個あたりの利益350円　販売個数100個
• コーヒー　1個あたりの利益100円　販売個数150個

売上1個あたりの平均の利益について考えていきます。この場合、シンプルに1個あたりの利益を足して2で割るだけでは不十分です。なぜなら、それぞれ販売個数に差があるためです。

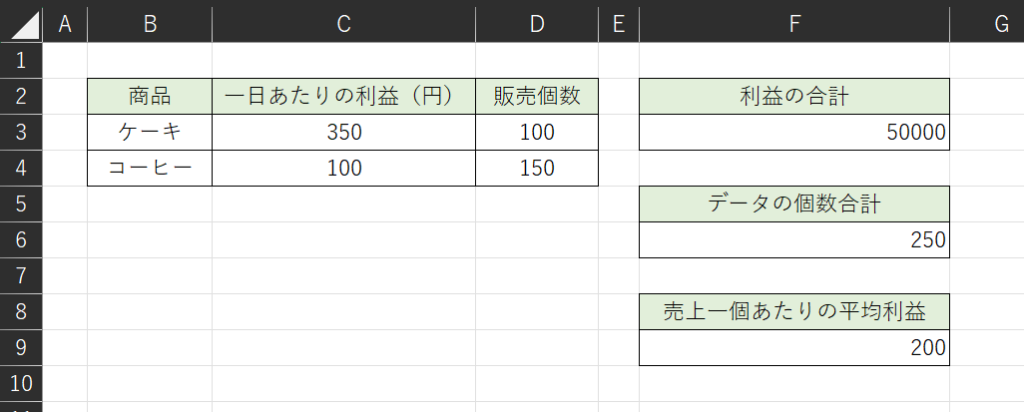
まずは、それぞれの利益の合計を算出します。

• ケーキの利益：350円×100個=35,000円
• コーヒーの利益：100円×150個=15,000円

35,000円+15,000円なので、利益の合計は50,000円ということが分かります。

そして、100個＋150個で、合計の個数は250個なので、1個あたりの平均利益は50,000円÷250個で＝200円となります。

これが加重平均の考え方です。

加重平均のExcelでの求め方

加重平均は関数で直接は求められないのですが、SUMPRODUCT関数を使うことで計算をスムーズに出来ます。

SUMPRODUCT関数では、たとえば以下のように選択することで「ケーキの利益×ケーキの販売個数」＋「コーヒーの利益×コーヒーの販売個数」の合計を簡単に求めることが出来ます。

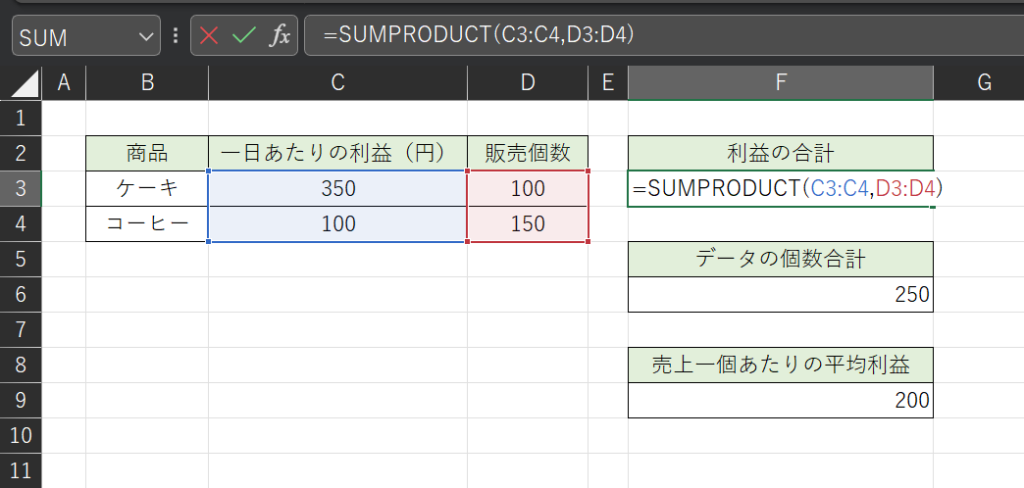
あとは、データの個数で割るだけで加重平均を求めることができます。

幾何平均とは

幾何平均は、平均の伸び率を表す場合に使われる平均です。

具体的には、企業の業績の上昇率をみるときなどによく使われます。

たとえば、A社では、2月の売上は1月の20％増、3月の売上は2月の40％増だったとしましょう。

このような場合の1月～3月の平均の売上上昇率を求めるとき、幾何平均が役に立ちます。

1月の売上を1とおくと、2月の売上は1月の20％増なので、1.2になります。

そして、3月の売上は2月の40％増なので、1.2×1.4＝1.68となります。

そして、求める月間の平均売上上昇率をaとおくと、1×a×a＝1.68となるので、これを解くと答えが出てきます。

（7月→8月、8月→9月で実際の伸び率は異なりますが、今回求めるのが平均の上昇率なので、同じaでおいています。）

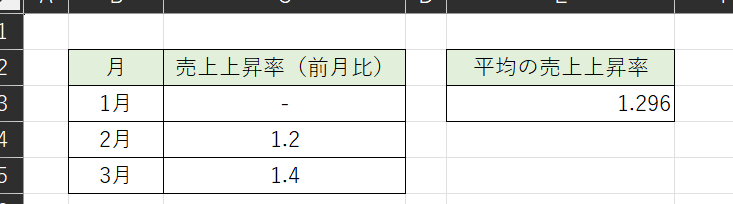
この式を解いていくと、「a²＝1.68」→「a≒1.296」となります。

よって、月間平均売上上昇率29％ということが分かりました。これが幾何平均の考え方です。

幾何平均のExcelでの求め方

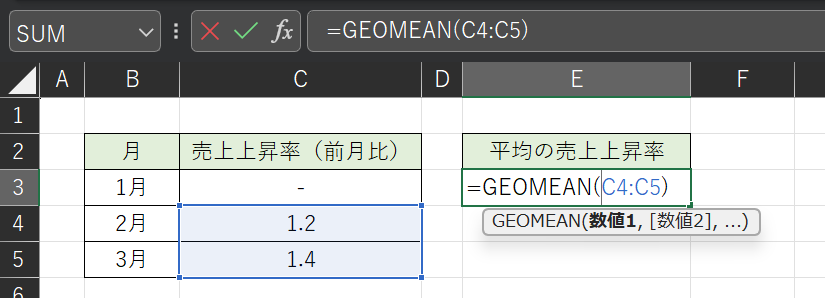
幾何平均は、GEOMEAN関数を使うことで求めることが出来ます。

以下のように対象の範囲を選択するだけで、簡単に幾何平均を算出できます。

業績や売上などの平均上昇率などをみたい場合に便利な関数です。

ビジネスでよく用いられるCAGR（年平均成長率）とは

幾何平均はビジネスにおいてもよく用いられる考え方で、有名なものがCAGRです。CAGRとは日本語では「年平均成長率」という意味で、その名前の通り1年間の平均成長率を示す値のことです。

今回の例では月ごとの売上データを例に解説しましたが、年ごとのデータで幾何平均を求めると、その値がCAGR（年平均成長率）となります。CAGRをはじめとした幾何平均の考え方は、将来の売上高を予測する際などに活用できるためビジネスにおいても重要な考え方となっています。

調和平均とは

調和平均は、比率に関する平均です。

調和平均は、速さの平均を計算する際に使われる平均です。

速度の平均は単純な算術平均で求めることはできません。たとえば、時速30kmと時速70kmでの平均は時速50kmというふうにはできません。

調和平均は、少し式がややこしいのですが、「データ数÷（それぞれ値の逆数の合計）」という式で求めます。たとえば3,5,7というデータがあったときには、「3÷（1/3+1/5+1/7）」というイメージです。

以下のような例で考えてみましょう。

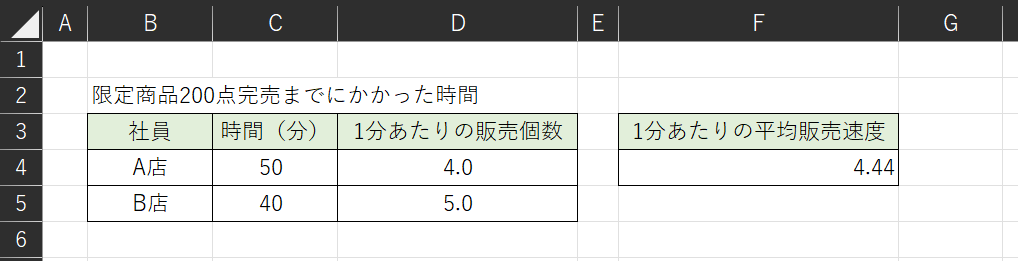
「とある限定商品200点をそれぞれA店とB店の2店舗で販売した。A店は完売までに50分かかり、B店は完売までに40分かかった。1分あたりの平均販売速度を求める。」

この場合、A店では200点を50分なので、一分あたりの販売個数は4個です。そして、B店では200点を40分なので、1分あたりの販売個数は5個です。

このふたつ調和平均は、2÷（1/4+1/5）なので、A店とB店の平均販売速度が4.44であることが分かります。

調和平均のExcelでの求め方

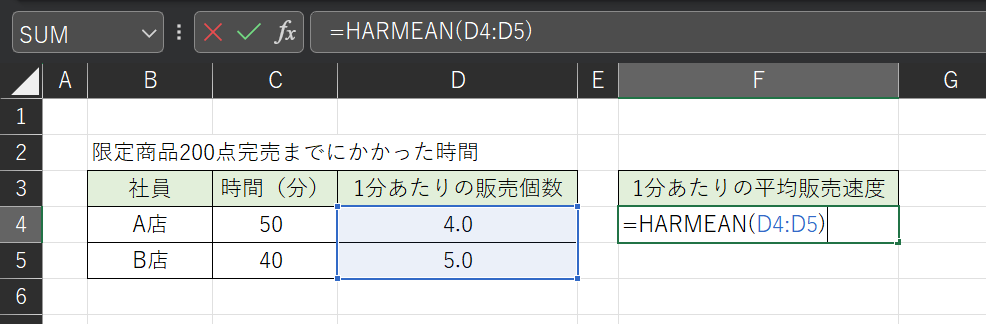
Excelで調和平均を求める場合は、HARMEAN関数を使います。

以下のように、HERMEAN関数で速さのデータを選ぶだけで算出されるので簡単です。

まとめ

一般的に「平均」というと、“データの合計÷データの個数“の算術平均を示すことがほとんどです。

算術平均は、ExcelではAVERAGE関数を使うことで求めることが出来ます。

また、平均には様々な種類のものがあり、例えば「加重平均」「幾何平均」「調和平均」などがあります。

場面によって適切な平均を選ぶ必要がありますので、是非それぞれの平均についても覚えておいてください。

＼ この記事を読んだ方におすすめ！ ／