この記事ではt検定の使い方やExcelでの活用方法を解説します。
\ DX推進のお悩みお気軽にご相談ください /

目次
この記事を読んだ人がよくダウンロードしている資料
t検定とは
t検定とは、t分布を利用した仮説検定の総称です。
※t分布・・・統計的検定でよく利用される分布の一つです。形としてはグラフの山が1つで左右対称のため、最も一般的な分布とされている正規分布と似ています。
※仮説検定・・・とある仮説が正しいのかどうかを統計学的に検証すること
簡単にイメージをお伝えすると、2つのグループの平均に有意な差があるかどうかを検定する手法です。
t検定は、母分散が未知の場合に用いられます。ビジネスの現場では、母分散があらかじめ分かっていないケースも多いので、使われる場面も多い検定手法といえます。
t検定のメリット
平均値の差が有意かどうかを判断できる
t検定を行うことで、2つのグループの平均値の差が有意なものかどうかを判断することが出来ます。
たとえば、薬投薬前と後での効果の比較、配信コンテンツAとBのCTRの比較、工程改善前と後での生産性の比較、などビジネスにおいても様々な場面で活用することが出来ます。
平均値はそれぞれのグループで異なることがあっても、それが誤差の範囲の可能性もあります。そのため、統計的な有意な差なのかどうかをしっかりと評価することで、正しく打ち手へと繋げることができます。
t検定の注意点
先述の通りt検定はt分布を使った検定ですが、t分布は自由度が大きくなると、正規分布に近似していく性質があります。
そのため自由度が大きいときにはt検定は使われません。
※自由度・・・サンプル数から1を引いたもの
明確な基準はありませんが、標本が30未満の場合にt検定を使うケースが多いので、こちらも一つの目安として覚えておきましょう。
t検定の種類
t検定は、大きく分けると、以下の3種類があります。
- 対応がある場合のt検定
- 分散が等しい場合のt検定
- 分散が異なる場合のt検定(Welch法)
どのt検定を行うかは、以下の要素によって変わってきます。
- 対応があるかないか
- 2つの母分散が等しいか、等しくないか
ちなみに、2つの母分散が等しいかどうかについては、F検定という手法を使って調べます。
※F検定については、以下の記事をご覧ください。
F検定とは Excelで分析を行う方法とともに解説
以下の表を参考に、どのt検定を実施すればよいか選んでみてください。

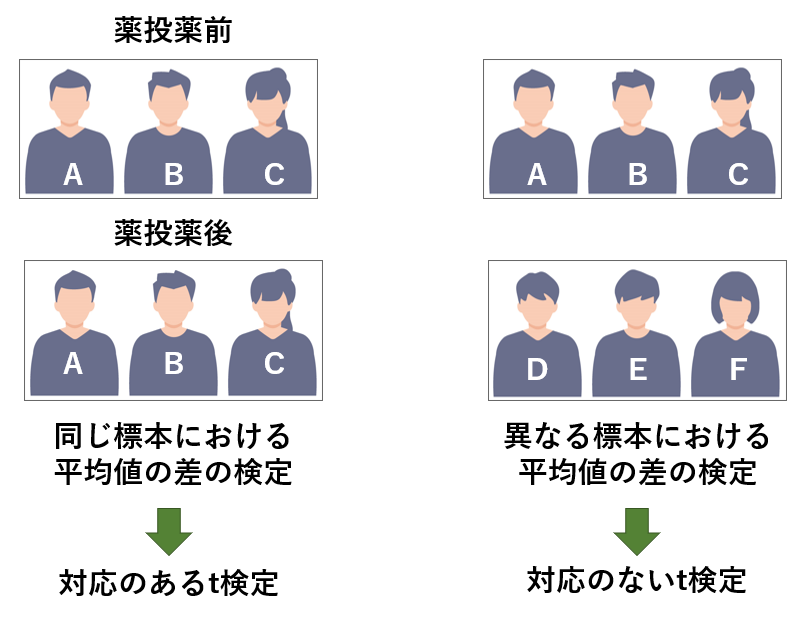
対応がある、対応がないとは
対応があるというのは、同じ人が複数回テストしたような場合のことを指します。たとえば、同一の人物に対して薬を投薬する前と後で検定をする場合は、「対応がある」ということになります。
一方、対応がないとは、異なる人で複数回テストしたような場合を指します。
t検定の分析手順
ここからは、Excelでt検定を行う方法をご紹介します。ちなみに、これから紹介する分析手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。
t検定は以下の手順で進めていきます。
- 帰無仮説と対立仮説をたてる
- 有意水準を設定する
- 検定統計量(t値)を算出する
- p値を求める
- 有意差を判定する
実際に行ってみないとなかなかイメージが湧きにくいかと思いますので、Excelで行う方法を見ていきましょう。
以下は、データ分析アドインが入っている前提で進めていきます。
データ分析アドインの設定がまだの方は、以下の記事を参考に設定のうえ、進めていただければと思います。
(参考)回帰分析とは 特徴やExcelでの分析方法を分かりやすく解説
Excelでt検定を行う方法(対応のある場合)
今回は、ダイエットサプリを飲む前と後での体重についてのt検定を行い、サプリの影響を調べてみます。
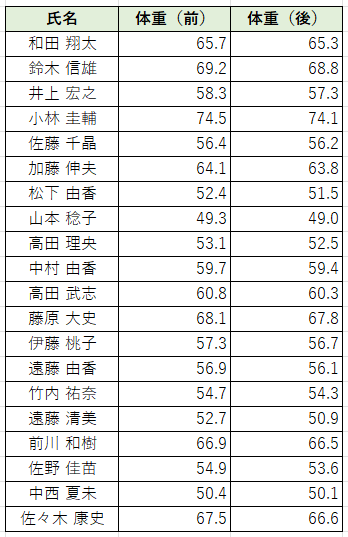
まずは、「①帰無仮説と対立仮説をたてる」を行います。
今回の場合は、ダイエットサプリに体重減少の効果があったのかをみたいので、以下のような仮説を設定します。
・帰無仮説:ダイエットサプリに体重減少の効果がない
・対立仮説:ダイエットサプリに体重減少の効果がある
帰無仮説はわかりやすくいうと「否定したい仮説」で、今回だと「ダイエットサプリに体重減少の効果がない」を否定することで、「ダイエットサプリに体重減少の効果がある」という仮説を説明していくイメージです。
続いて、「データ」→「データ分析」→「t検定:一対の標本による平均の検定」とExcelの画面を進めていきます。

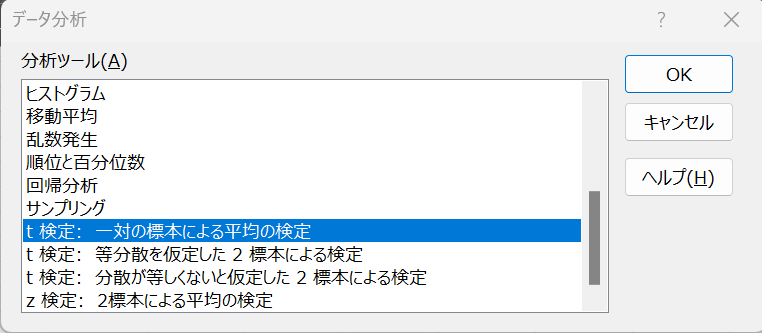
そして、出てきたポップアップに沿って、必要な情報を入力していきます。
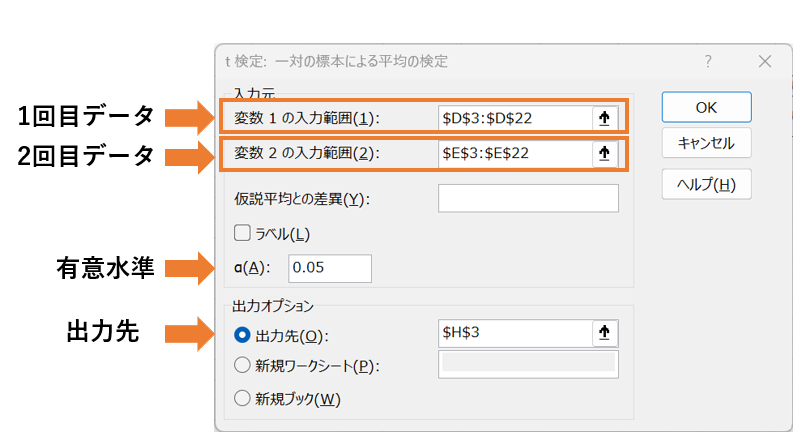
「入力範囲」には対象となる元データがあるセルを選択します。
必要に応じて、「先頭行をラベルとして使用」にチェックをつけます。
「α」は有意水準という、p値がどれくらい小さいときに有意差があるかを判断する値です。特に理由がなければ、デフォルトの0.05のままで進めていきます。(「②有意水準を設定する」に該当する部分です。)
※p値・・・帰無仮説のもとで、その事象が起こる確率のこと。
最後に出力先を選び、「OK」をクリックすると、以下のような分析結果が出力されます。
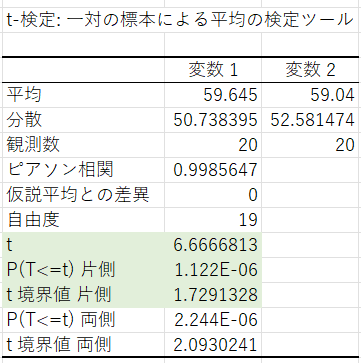
これで「③検定統計量(t値)を算出する」、「④p値を求める」まで完了しました。
あとは、出力結果を読み取って「⑤有意差を判定する」をしていきます。
今回は「体重減少の効果の有無」を見るので、片側検定の数値を見ていきます。
※体重増加については考えないので、片側検定となる。もし「体重の変化」を考える場合は、減少・増加の両方を考えることになるので、両側検定となる。
まず、「t境界値片側」より、棄却域が「t >1.73」と分かります。
そして選択したデータから計算した「t値」は6.7となっており、t値が棄却域に入っていることが分かります。
そして「P(T<=t) 片側」(片側検定の場合にみるp値)が0.05以下となっていることから、この平均値の差が統計的に有意であることが分かります。
よって、帰無仮説は棄却され「有意差が認められる」という結果になりました。
つまり、このダイエットサプリは、体重減少の効果があるといえます。
Excelでt検定を行う方法(対応のない場合)
次に、対応のない場合のt検定の方法をご紹介していきます。
まずはF検定を行い、「分散が等しい場合のt検定」か「分散が異なる場合のt検定」のどちらを使うかを確認したうえで進んでいきます。
分散が等しい場合のt検定
以下は、とある会社の男性と女性の年収のデータです。
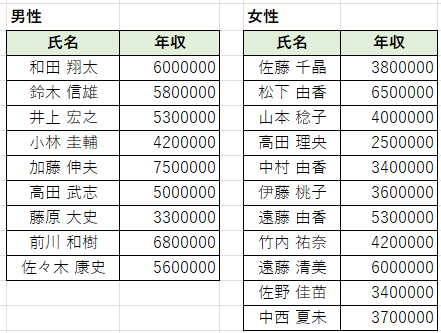
まずは、仮説を立てます。
・帰無仮説:男女間で年収に差がない
・対立仮説:男女間で年収に差がある
そして「データ」→「データ分析」→「t検定:等分散を仮定した2標本による検定」と進んでいきます。

あとは、対応ありデータと同様に、必要なデータを入力していきます。
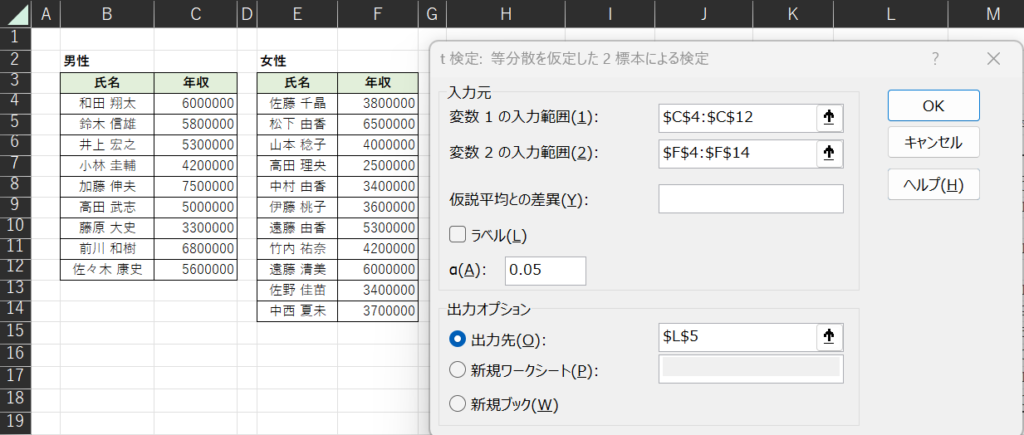
データを入力しOKをクリックすると、以下のような結果が出力されます。
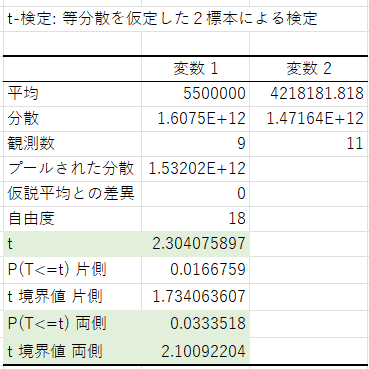
今回は「男女間で年収に差があるか」を見るので、両側検定の数値を見ていきます。
まず「t境界値両側」より、棄却域が「 | t |>2.1」と分かります。
そして選択したデータから計算した「t値」は2.3となっており、t値が棄却域に入っていることが分かります。
そしてp値が0.05以下となっていることから、この平均値の差が統計的に有意であることが分かります。
よって、帰無仮説は棄却され「有意差が認められる」という結果になりました。
つまり、この場合男女間で年収の差があるといえます。
分散が異なる場合のt検定(Welch法)
以下は、先ほど同様の年収データの数値を変更したものです。
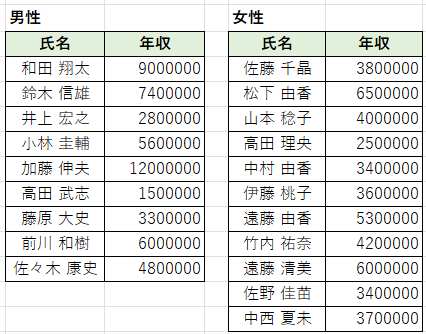
まずは、仮説を立てます。
・帰無仮説:男女間で年収に差がない
・対立仮説:男女間で年収に差がある
そして「データ」→「データ分析」→「t検定:分散が等しくないと仮定した2標本による検定」と進んでいきます。
データ入力の方法は、「分散が等しい場合のt検定」と同様なので割愛します。
分析の結果、以下のようなデータが出力されました。
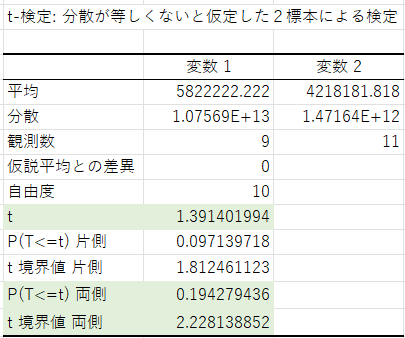
今回は「男女間で年収に差があるか」を見るので、両側検定の数値を見ていきます。
まず「t境界値両側」より、棄却域が「 | t |>2.2」と分かります。
そして選択したデータから計算した「t値」は1.3となっており、t値が棄却域に入っていないことが分かります。
また、p値が0.05よりも大きいため、帰無仮説を棄却することができず、この平均値の差が統計的に有意ではないことが分かります。
つまりこの場合、男女間で年収に有意な差があるとはいえません。
ビジネスにおけるt検定の活用イメージ
ここからは、ビジネスにおいてt検定の活用イメージをご紹介します。
ケース1 アンケート結果の分析

たとえば、マーケティングのために顧客から取得したアンケート結果を分析する際にも活用することが出来ます。
アンケート結果で差が出たときにも、果たしてその差が有意な差と行ったも良いものなのか、もしかしたら誤差と言える範囲ではないのか、などを検証する際にt検定を活用することが出来ます。
ケース2 新薬の効果を確かめる

たとえば、治験で得られたデータをもとに、新薬の効果を確かめる場合にもt検定を活用することが出来ます。
グループごとでの効果の差を比較してみたり、投与前、投与後の差についてt検定を行うことで、新薬により有意な差が見られたのかを調べることも出来ます。
ケース3 コンテンツの閲覧率の分析
マーケティングの場面でもt検定を活用することができます。
たとえば、ある顧客のリストに対して、1年間のあいだ毎月メルマガ配信をするとします。
その際、カテゴリAとカテゴリBの異なるカテゴリのコンテンツを用意し、そのクリック率を記録していきます。そうして記録したクリック率の平均値を取ったときに、クリック率がカテゴリAは15.2%、カテゴリBは14.7%でした。
平均値だけ見るとカテゴリAの方が良い結果のように思えるかもしれませんが、この平均値の差は誤差の範囲で、統計的に意味のある差ではない可能性もあります。
このように、このクリック率の平均値の差が意味のあるものなのかを確認するときにt検定を使うと効果的です。
t検定の結果有意な差が見られた場合は、カテゴリAのコンテンツの方が関心度が高いということで配信内容をそちらに寄せていくなど。様々な打ち手に繋げていくことが出来ます。
マーケティング施策の有用性を図ることで、より最適なマーケティンを行うことができるようになりますので、是非活用してみてください。
ケース4 工場における生産管理
t検定は工場における生産管理にも活用することができます。
たとえば、工程を改善する前と後で、生産量の平均値に差があるのかどうかをみることで、工程改善に意味があったのかどうかを統計的に判断することができます。
まずは一つの現場で改善を試してみて、統計的に有意に生産性が改善された場合は、他の現場にも展開していくという方法もよいでしょう。
統計的な根拠を持って説明された方が、現場の方々にも納得して動いてもらいやすいというのもデータ分析を行うメリットです。
まとめ
t検定を使うことで、平均値の差が有意な差なのかどうかを確認することができます。
データ分析に慣れていないと最初は少しとっつきにくいかもしれませんが、使いこなせると便利な手法ですので、是非この機会に覚えておきましょう!
\ この記事を読んだ方におすすめ! /