F検定とは Excelで分析を行う方法とともに解説
目次
この記事を読んだ人がよくダウンロードしている資料
F検定とは
F検定とは、等分散の検定の一種です。
「等分散の検定」というと少し難しく聞こえるかもしれませんが、簡単にいうと、2つのグループ（群）の母分散（ばらつき）が、等しいか、等しくないかを判定するときに使う分析手法です。
（※母分散・・・母集団の分散。観測対象全体のデータのばらつき具合。）
F検定は、t検定の事前検定として使われる
F検定は、t検定を行う前に実施する、いわゆる事前検定として利用されるケースが多い検定です。
対応のないt検定を行う場合、母分散に差があるかないかで、実施するt検定の種類が変わってきます。
・母分散が等しいと仮定→分散が等しい場合のt検定（Welchのt検定）
・母分散が等しくないと仮定→分散が等しくない場合のt検定
※t検定について、詳しくは以下の記事をご確認ください。
t検定とは Excelで分析を行う方法を解説
グループ間の母分散が等しいかどうかを分析し、どちらのt検定を使うかを判断するために使われることが多いのがF検定です。
F検定の分析の手順
F検定は、以下の手順で進めていきます。
- 仮説を立てる
- 有意水準を決める
- 検定統計量（F値）を算出する
- p値を算出する
- 有意差を判定する
実際にExcelで分析する手順を見ていきましょう。
※ここからは、Excelにデータアドインツールが入っている前提で説明しています。もし設定がまだの方は、以下の記事で解説しているので、参考にしながら設定のうえ進んでください。
（参考）回帰分析とは 特徴やExcelでの分析方法を分かりやすく解説
ExcelでF検定を行う方法
ここからは、ExcelでF検定を行う方法をご紹介します。ちなみに、これから紹介する分析手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。
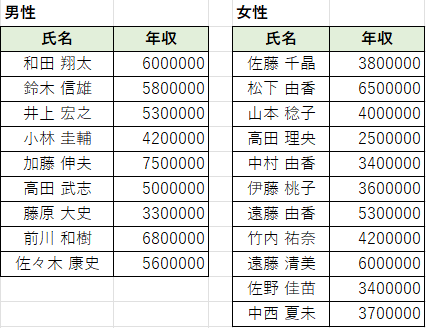
今回は以下のような、とある集団における男女別の年収データに対して、F検定を実施していきます。
仮説を立てる
まずは、「①仮説を立てる」です。
F検定の場合の仮説は、母分散が等しいかどうかをみる検定ですので、以下のように仮説を設定します。
・帰無仮説：2群の母分散が等しい
・対立仮説：2群の母分散が等しくない
有意水準設定、 検定統計量（F値）とp値の算出
次に、「②有意水準の設定です。」
まず、「データ」→「データ分析」→「F検定：2標本を使った分散の検定」と進んでいきます。
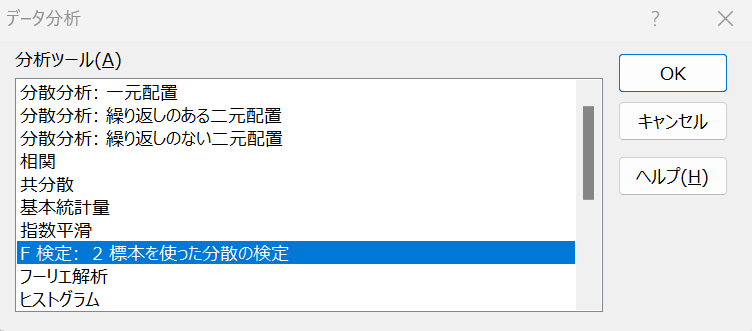
そして出てきたポップアップに沿って、必要な情報を入力していきます。
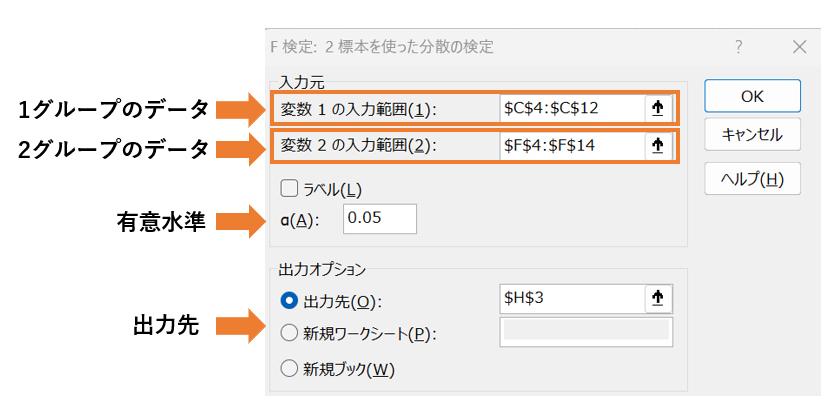
変数1と2の入力範囲には、それぞれ2群のデータの範囲を入力していきます。
また、有意水準（有意差を判定する基準）は、一般的によく使われる0.05（5％）がデフォルトで入っているので、特に理由がなければそのままで問題ありません。
最後に、分析結果の出力先を選んで「OK」をクリックします。
すると、以下のような出力結果が出てきました。
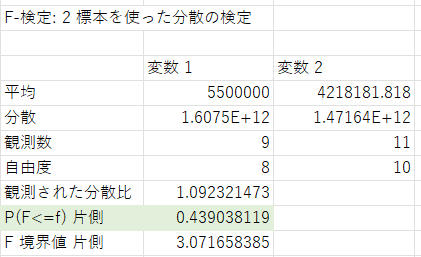
これで「③検定統計量（F値）を算出する」「④p値を算出する」が完了です。
有意差の判定
最後に、結果から「⑤有意差を判定する」を行っていきます。
まず、「P(F<=f)片側」より、p値が0.44と読み取れます。
p値が有意水準の0.05よりも大きいため、今回の場合、帰無仮説は棄却されません。
つまり、母分散に差はないとみなせる（母分散は等しいと仮定できる）という結論になります。
（参考）等分散でない場合のイメージ
また、参考に等分散でないケースも見ていきましょう。
少し年収の数値を変えた、以下のようなデータでF検定を実施してみます。
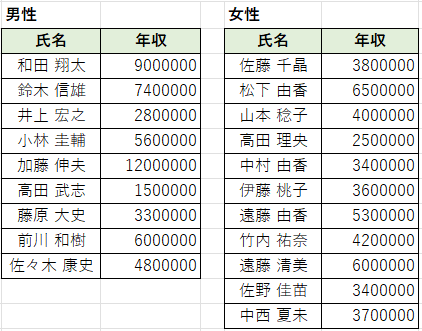
上記と同じ手順でF検定を実施すると、出力された結果は以下の通りでした。
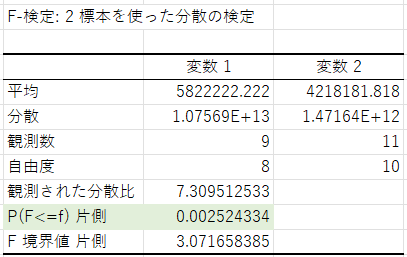
この場合、p値が0.0025ということで5％未満です。
つまり、この場合は帰無仮説を棄却することが出来るので、差があるといえる（等しくないと仮定できる）という結論になります。
ビジネスにおける活用イメージ
先ほどF検定はt検定の前の事前検定として使われるとお伝えしましたが、単純にばらつき具合を比較したい場合にも活用できます。
ビジネスでの活用イメージを１つご紹介します。
ケース：営業所の成績を比較
たとえば、A株式会社では、契約件数が同じくらいの東京と大阪の２つの営業所があったとします。
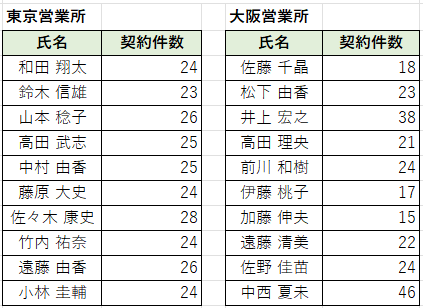
この２つの営業所と各営業担当の契約件数についてF検定を行った結果、大阪営業所は東京営業所とでは、各営業担当ごとでの契約件数のばらつき具合に有意な差があるということがわかりました。
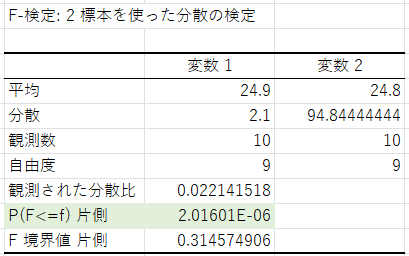
詳しくデータを見てみると、以下のような理由でばらつき具合に差が出ていることがわかりました。
- 東京営業所
→皆が同じくらい成果を上げている - 大阪営業所
→何人かの営業担当が突出して成果を上げており、その他の営業担当は成果を上げられていない
差が出ている理由を調べたところ、どうやら東京と大阪とで中途入社の営業社員の研修内容に違いがあるではないかと予想しました。
そこで、大阪営業所で行われている研修の内容を再確認し、皆がしっかり成果を上げられるように再度研修に取り組みました。
その結果、大阪で成果を上げられなかった社員たちも成果を上げられるようになり、契約件数の全体の底上げとなり、売上が改善されました。
今回は、営業所ごとの営業担当における契約件数のばらつきで考えてみましたが、ほかにも応用できます。
たとえば、キャンペーン実施前と後での売上のばらつきの比較であったり、営業所でグループ分けするのではなく男女別での比較で売上を比べてみるなどがありますね。
自社ではどんな活用ができるか、考えてみてください。
まとめ
まとめると、F検定を使うことで「2つの集団の母分散に差があるといえるのかどうか」を判断することが出来ます。
これは対応のないt検定を実施するうえで、重要になってくる作業です。
t検定を使ってデータ分析を行いたい方は、あわせてF検定の手順も覚えておきましょう！
＼ この記事を読んだ方におすすめ！ ／
