今回は統計学で使われる「最小二乗法」とは何なのか、どのようにして求めるのか、活用場面などをご紹介していきます。

＼ この記事を読んだ人がよくダウンロードしている資料（無料） ／

最小二乗法とは

この記事では、最小二乗法について詳しくご説明します。

最小二乗法は、データとそれを表す回帰直線の誤差を最小にするような直線y=ax+bの回帰係数ａと切片bを決める方法のことです。

具体的には、残差の二乗和が最小になるようなもっとも当てはまりのいい回帰直線を求める方法です。

字面だと少しイメージがしにくいかもしれないので、図を用いてご説明します。

最小二乗法のイメージ

たとえば、以下のような12個のデータがあったとします。

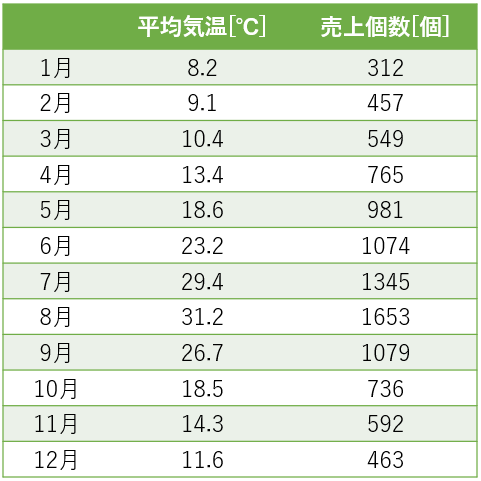
このデータは、架空のアイスクリーム屋における、気温とアイスクリームの売上個数のデータです。

このデータの特徴を把握しやすくするために、散布図に落とし込んだものが以下の図です。

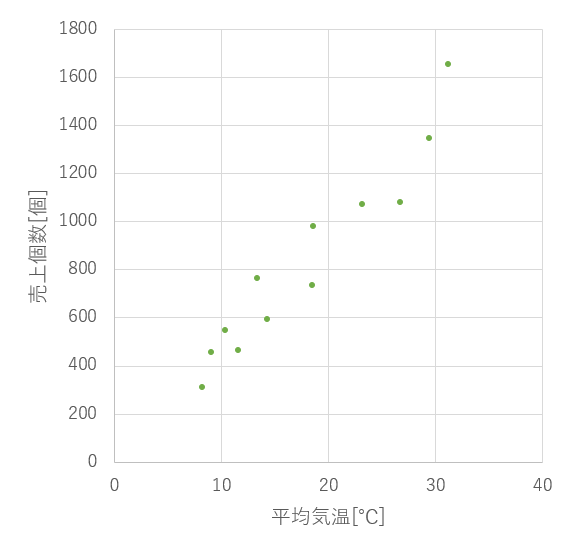
散布図をみると、このデータには直線的な関係が見られそうということがなんとなく分かるかと思います。

そこで、このデータにもっとも当てはまりそうな直線（もっとも誤差が小さくなる直線）を書いてみると、以下のようになりました。

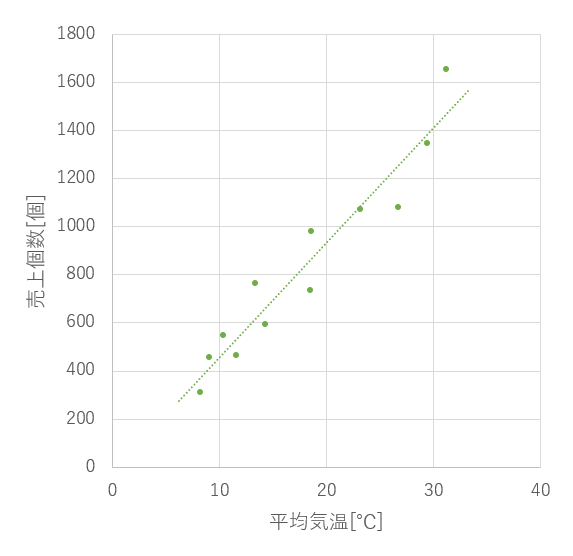
これが最小二乗法のイメージです。

最小二乗法で求められた回帰直線をみることで、変数間の特徴を直感的に把握できるようになります。

また、たとえば「気温が○℃のとき、売上個数はこれくらいになる」という将来の予測にも使うことができます。

最小二乗法は、回帰直線を求める時に使われる方法です。

回帰分析については、以下の記事で詳しく説明しておりますので、ご確認ください。

回帰分析とは　特徴やExcelでの分析方法を分かりやすく解説

Excelで最小二乗法による直線式を求める方法

ここからは、Excelで最小二乗法を行う方法をご紹介していきます。ちなみに、これから紹介する手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。

LINEST関数で求める方法

Excelで最小二乗法を行う場合、LINEST関数を使います。

関数の式は以下のように入力していきます。

=LINEST（Yの範囲、Xの範囲、切片を0にするかどうか）

まず、Excel上にデータを用意します。

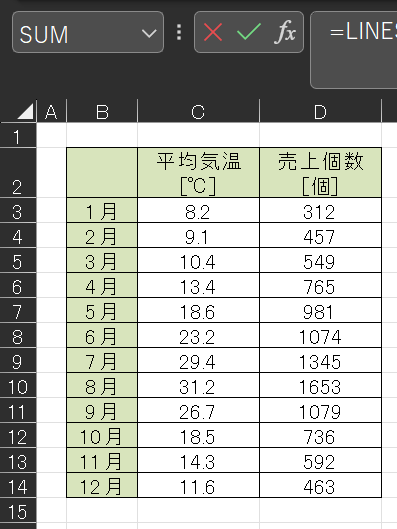
ここでは、

• Yの範囲：売上個数
• Xの範囲：平均気温
• 切片を0にするかどうか：0にしない

として求めていきます。

今回の場合は、「=LINEST(D3:D14,C3:C14,TRUE)」と入力しています。

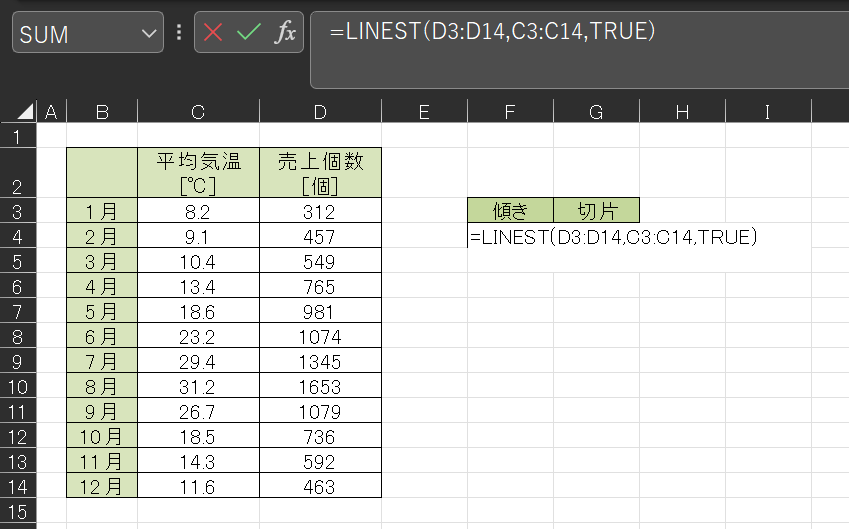
入力してEnterを押すと、以下のように計算結果が出てきます。

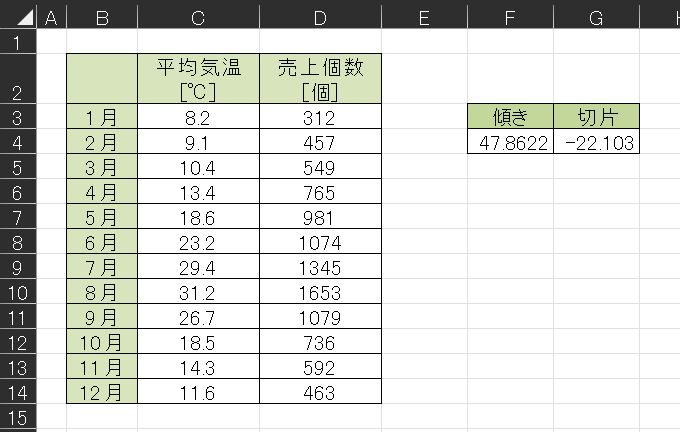
これで、平均気温と売上個数のデータの回帰直線の傾きと切片を求めることが出来ました。

散布図から確認する方法

散布図を作って、そこから回帰直線の傾きや切片を把握することも可能です。

まずは、データを選択したうえで、「挿入」→「散布図」と進めていきます。

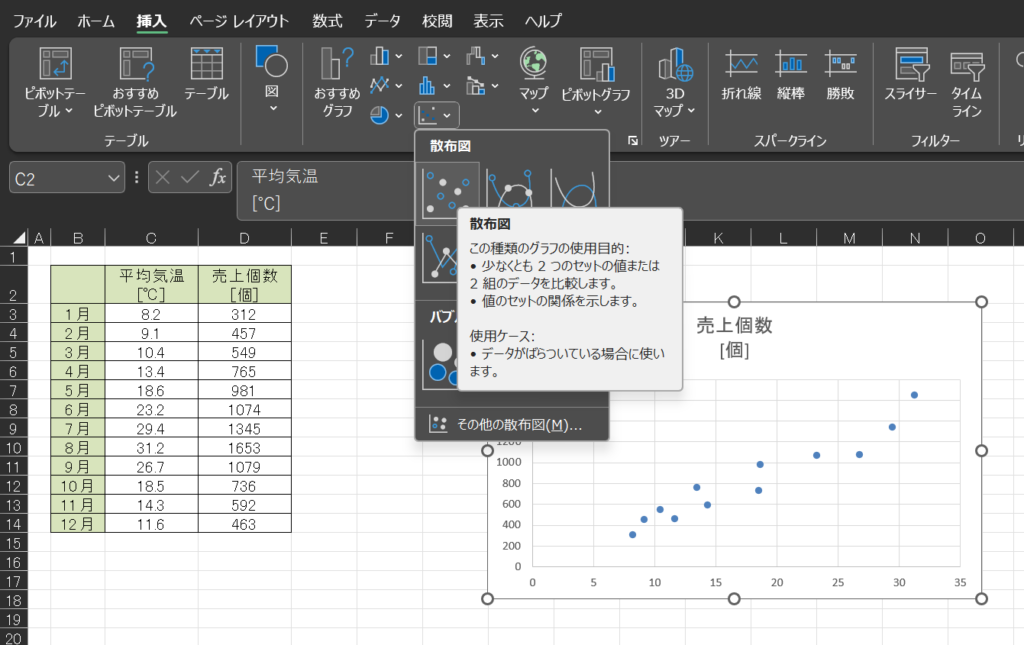
そうすると、散布図が出来てきます。

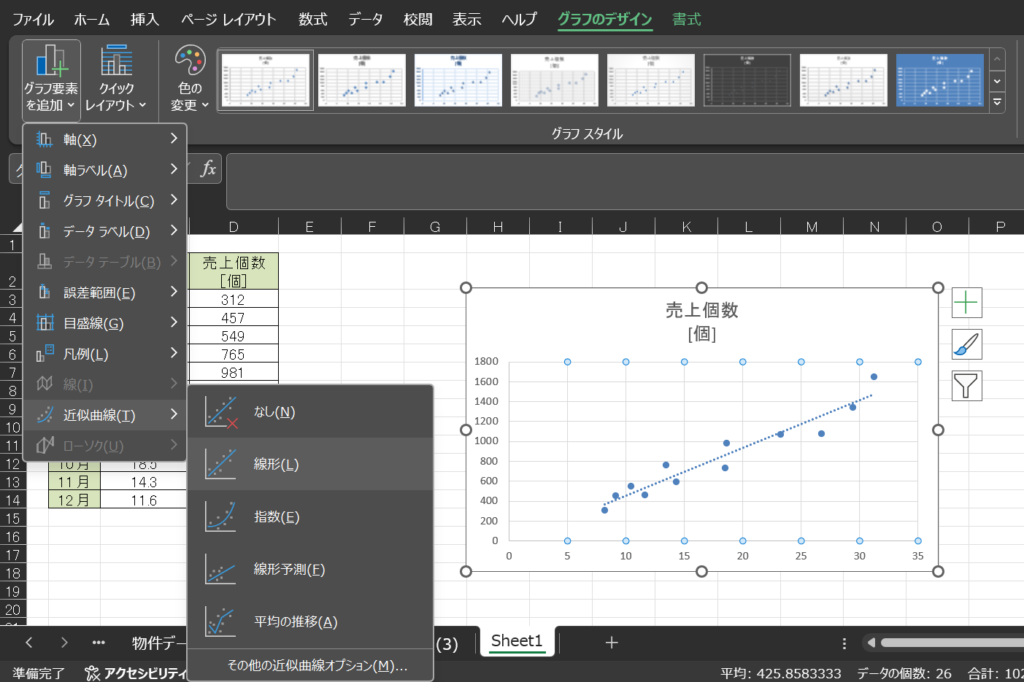
出てきた散布図を選択して、「グラフのデザイン」→「近似曲線」→「線形」を選びます。

そうすると、以下のようにグラフ上に回帰直線が出てきます。

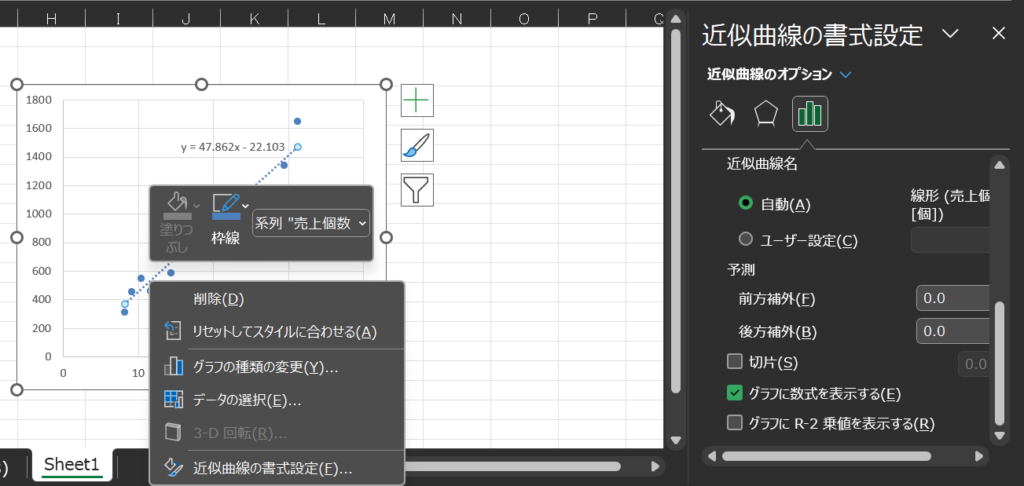
続いて、グラフをクリックして、右クリックで「近似曲線の書式設定」を開きます。

近似曲線の書式設定のなかにある「グラフに数式を表示する」にチェックを入れます。

そうすると、以下のようにグラフ内の直線に数式が表示されます。

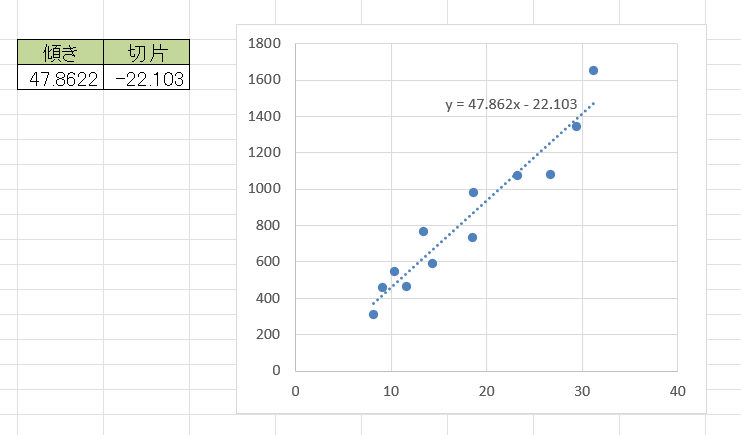
LINEST関数で求めた傾きや切片と一致していますね。

このようにして切片や傾きを確認することもできます。

最小二乗法の活用事例

先ほど求めた架空のアイスクリームの売上について、気温をもとに予測していきます。

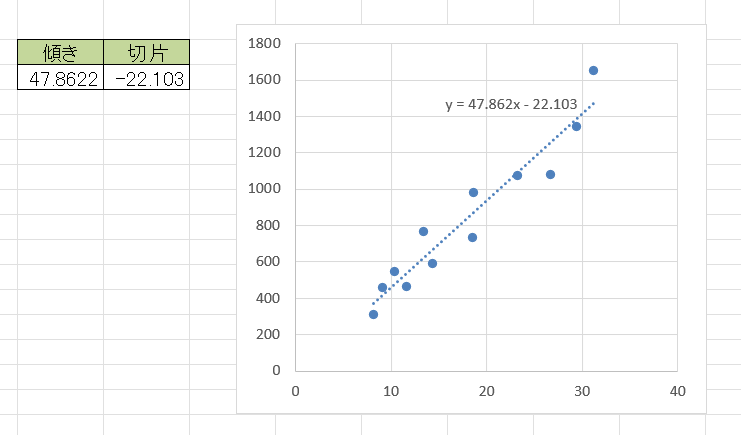
先ほど「y = 47.862x – 22.103」という式が求められました。

今回、平均気温(ｘ)が20℃のときにどれくらいの個数売れるのかを予測していきます。

そこで、式のなかの「x」に20を入れて計算していきます。

そうすると、「47.862×20-22.103＝935.137」と計算することが出来ます。

つまり、20℃のときにはおよそ935個程度売れると予測出来るということです。

ここから、「余裕をもって1000個程度の在庫は用意しておいた方がいいかな」といった予測ができます。

このように過去の実績をもとに計算することで、なんとなく「これくらいだろう」と勘で準備する場合に比べ、適切な量の在庫を準備しておくことが出来るので、廃棄を少なくすることができます。

また、不要に冷蔵庫や冷凍庫に在庫を置いておく必要もなくなるので、管理もしやすくなります。

このように、最小二乗法の考えに基づいた回帰分析を行うことで、将来の予測に非常に役立ちます。

実際、最小二乗法の関数だけを使うというよりも、回帰分析として使うケースが一般的です。

以下の記事で回帰分析の詳しい説明や活用事例をご紹介していますので、是非ご覧下さい。

回帰分析とは　特徴やExcelでの分析方法を分かりやすく解説

まとめ

今回は、最小二乗法についてご説明しました。

最小二乗法は、データとそれを表す回帰直線の誤差を最小にするような直線の係数（傾き、切片）を決める方法です。

最小二乗法について理解出来ると、回帰分析の分析結果の読み取りのイメージもしやすくなります。

是非この機会に覚えておきましょう。

＼ この記事を読んだ方におすすめ！ ／