この記事を読んだ人がよくダウンロードしている資料

分散分析とは

分散分析とは、簡単にいうと「3グループ以上の平均を比較し、有意差（統計的に意味のある差のこと）があるかを判断する分析手法」のことです。

このように、それぞれのグループの平均値の差について、その差が統計的に意味のある差なのかどうかを調べる手法のことを「平均値の差の検定」といいます。分散分析は平均値の差の検定の1種です。

分散分析とt検定の違い

平均値の差の検定といえばt検定がありますが、t検定は3グループ以上では使えない手法です。

そこで、3グループ以上の平均値の差の検定では分散分析という方法を使います。

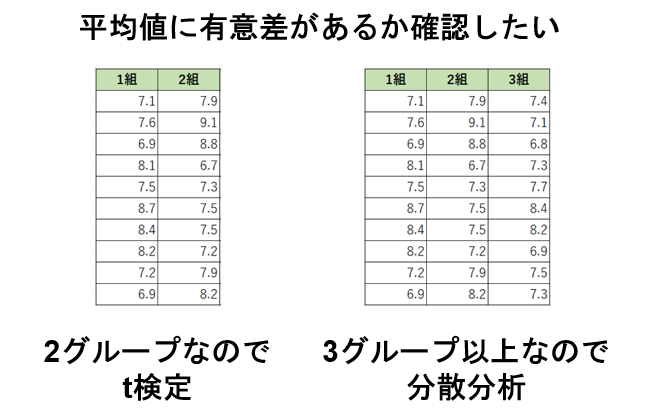
たとえば、北海道と沖縄の20代男性の平均体重に有意な差があるのかは、2グループの平均値の差の検定なのでt検定です。

徳島県、香川県、愛媛県、高知県の20代男性の平均体重に有意な差があるのかみたいという場合は、3グループ以上なので分散分析を行うということになります。

このようにデータのグループ（群）数に応じて使い分けをしていきます。

ちなみに、t検定は2つのグループの平均値に有意差があるかどうかを調べる手法のことです。t検定について詳しく知りたい方は、以下の記事をご確認ください。

『t検定とは Excelで分析を行う方法を解説』
t検定とは Excelで分析を行う方法を解説

分散分析のなかでも最も基本的なものが、一元配置分散分析とよばれるものです。

分散分析の注意点

分散分析で分かるのは、有意差があるかどうか

先述のとおりですが、分散分析で分かるのは、あくまでも全体の中のどこかに有意な差が存在しているかどうかだけです。

具体的にどのグループの間に差があるのかまでは分散分析の結果だけでは読み取ることができないので、覚えておきましょう。

データによって分散分析の種類が変わる

分析する対象のデータがどういったものかによって分散分析のなかでも種類が分かれてきます。

例えば、実験の目的となる要因が1つの場合に行う一元配置分散分析や、2つの要因を持つデータの場合は二元配置分散分析を行うといった分類があります。ほかにも、データに繰り返しがあるかないか（「繰り返し」についてはのちほど詳しく説明します）によっても変わってきます。

これらの使い分けについても、後ほど説明していきますが、分散分析を行うためにはこういったデータの見分け方も分かるようにしておくことが大切です。

分散分析の種類

分散分析には、一元配置分散分析、多元配置分散分析という種類があります。

一元配置分散分析とは、実験の目的となる要因が1つ（1元）の場合に行う分散分析です。

「1元」とは、” 要因が一つである ”とイメージしてもらえればわかりやすいと思います。（たとえば、「職業別」「年齢別」という2つの要因を持つデータの場合は「2元」となります。）

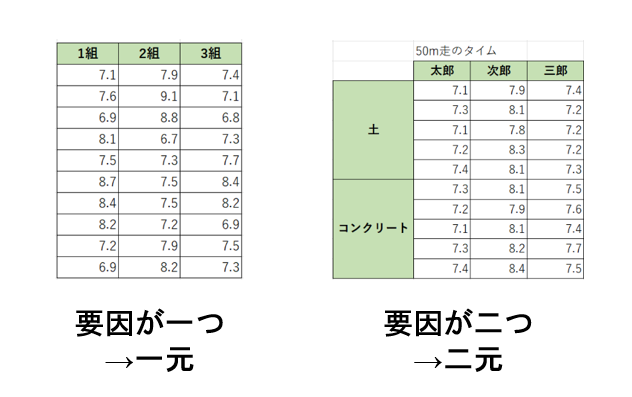
今回は、Excelで簡単に一元配置分散分析を行う方法についてご紹介していきます。

Excelで一元配置分散分析を行う方法

ここからは「分析ツール」アドインが追加されている前提で、Excelで一元配置分散分析を行う手順をご紹介していきます。

アドインの追加がまだの方は、以下の記事にて画像付きでご紹介していますので、まずはそちらをもとに設定をしたうえで解説に進んでください。

（参考） 回帰分析とは　特徴やExcelでの分析方法を分かりやすく解説

なお、これから紹介する分析手順に用いるExcelテンプレートはこちらから無料ダウンロード可能ですので、ぜひダウンロードして読み進めてみてください。

例題　3クラスの50ｍ走タイムの平均値に有意差があるか調べたい

今回は、とある学校における50m走のタイムについてクラス（1組～3組）間で有意な差があるかを見ていきたいと思います。

まずは、以下のような元データを用意します。

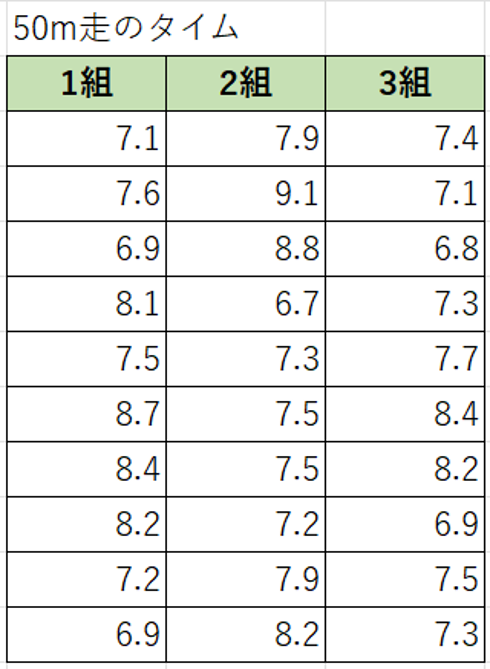
次に、「データ」 →「データ分析」とクリックし、

出てきたポップアップの中で「分散分析：一元配置」を選びます。（今回は要因が「クラス（1組、2組、3組）」の1つだけなので、1元になります）

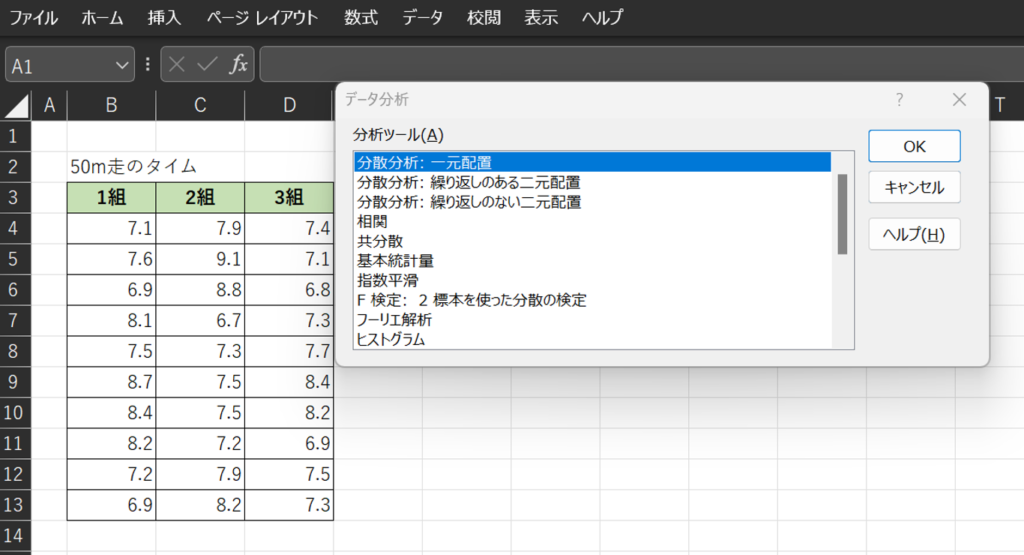
そうすると詳しい設定内容が出てくるので、

「入力範囲」には対象となる元データがあるセルを選択し、

「先頭行をラベルとして使用」にチェックをつけます。

「α」は有意水準というものを表しており、これはp値がどれくらい小さいときに有意差があるかを判断する閾値です。一般的には5％（0.05）と設定することが多いので、特に理由がない限りデフォルトの0.05のままで問題ありません。

※p値・・・帰無仮説（否定したい仮説）のもとで、その事象が起こる確率のこと。

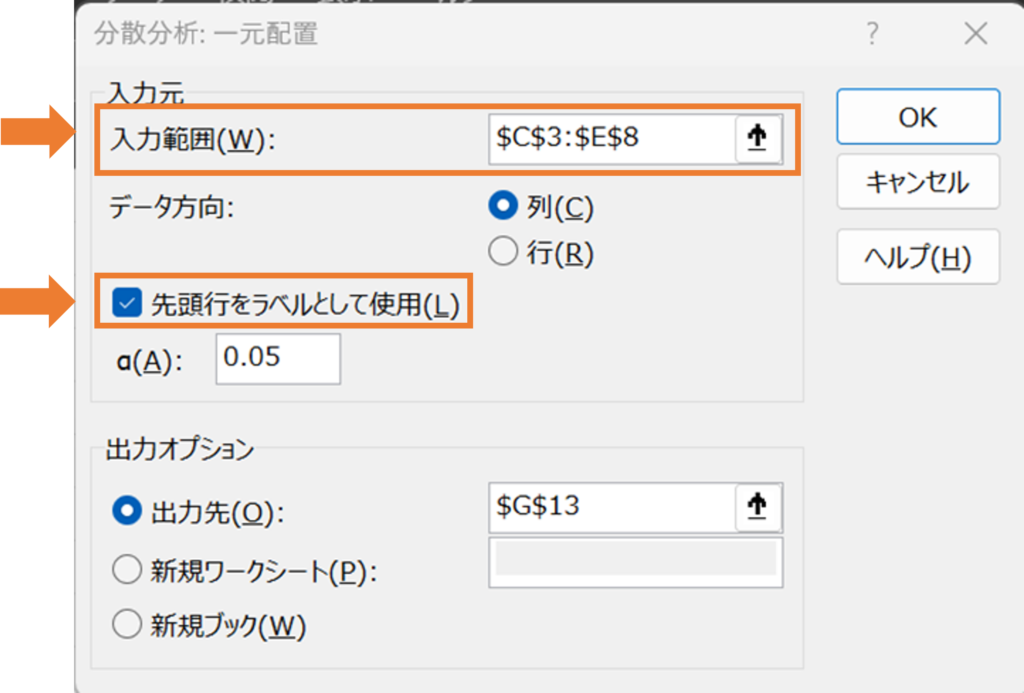
あとは出力先を選択し、「OK」をクリックします。

そうすると、以下のような分析結果が出力されました。

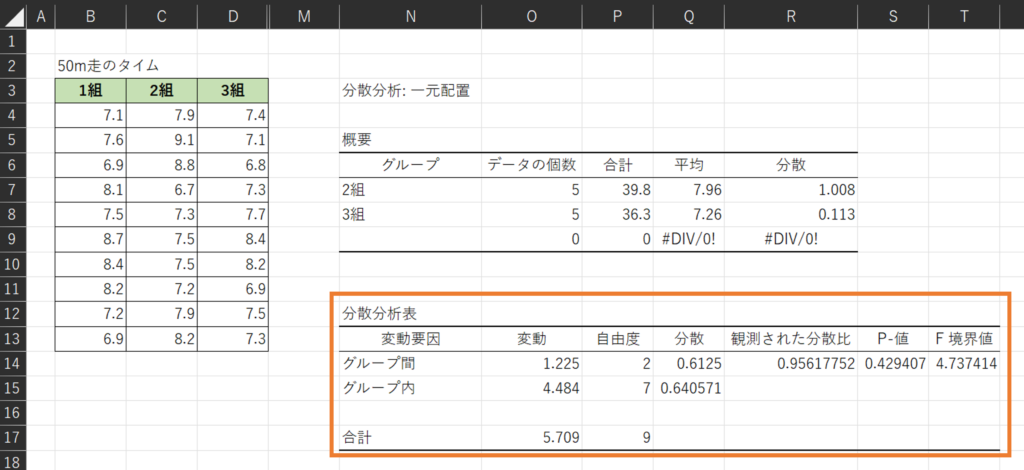
上にでている「概要」の表は、簡単な統計量をまとめたものであり、ここでは特に気にしなくても大丈夫です。

重要なのは下の「分散分析表」で、こちらの読み取りをしていきます。

t検定ではt値を使いましたが、分散分析の場合はF値という値を使います。

F値は、各データの分散比のことで、この値が大きいほどグループ間の平均値に差があるといえるといえます。

ちなみに、F値の計算式は、「各因子の平均平方÷残差の平均平方」ですが、こちらはExcelが計算してくれるのでビジネスで活用するだけであれば特に覚える必要はありません。

上の図にでてくる「観測された分散比」というのがF値のことなので覚えておきましょう。

そして特に大切なのは、p値です。

p値は、検定統計量（分散分析の場合はF値）をもとに算出する値です。

p値は有意確率のことで、詳しくいうと「帰無仮説が正しい前提において、それ以上に偏った検定統計量が得られる確率」のことです。

少し難しいかもしれませんので、一旦p値は「有意水準5％の場合、p値が0.05以下であれば有意差があるとみなせるもの」と認識しておけば大丈夫でしょう。

さきほど設定していた閾値0.05をp値が上回っていたため、3グループの平均値には有意差がないと判断できます。

二元配置の分散分析とは

ここまでは、1元配置の分散分析でしたが、二元配置の分散分析というものもあります。

これは名前の通り、要因が2つ（2元）の場合に行う分散分析です。

たとえば、「職業別」「男女別」を組み合わせたデータの平均値の差を知りたい場合には二元配置分散分析が適しています。

また、二元配置分散分析は、「繰り返しのある二元配置」「繰り返しのない二元配置」と分類出来ます。

これは元データが同一条件のなかで複数のデータが存在するかどうかの違いです。

例えば、以下の図のようなデータがあったとします。（土、コンクリートは走る環境の違いです。）

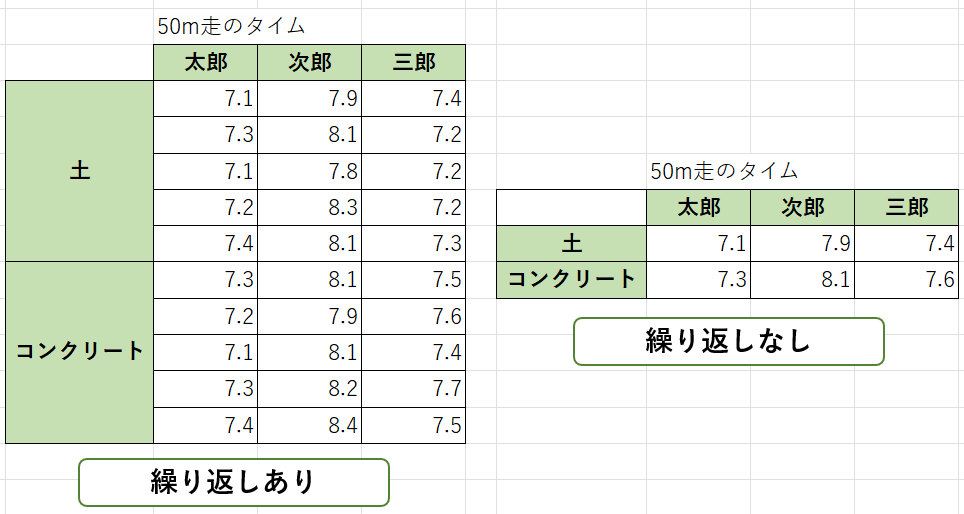
この場合、左の表には「太郎」×「土」といったように、同一条件のなかで複数のデータを持っています。一方、右の表では一つの条件においてデータが一つです。

左のようなデータだと「繰り返しあり」ですが、右のようなデータだと「繰り返しなし」となります。

二元配置の分散分析（繰り返しなし）の場合

二元配置になっても、基本的に分析の手順は同じです。

「データ」→「データ分析」と進み、対応した分析手法を選んでください。

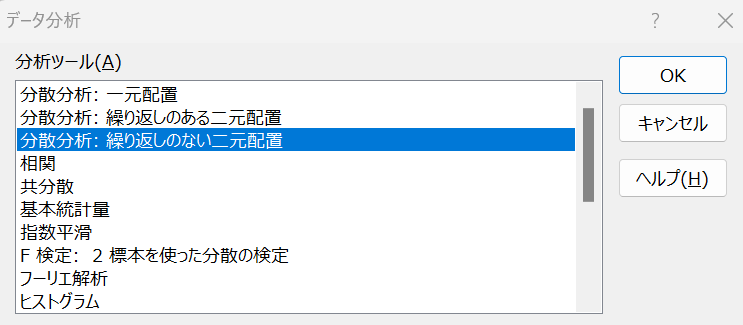
あとは、設定画面で元データの範囲を選び「OK」をクリックします。

そうすると、以下のような分析結果が出てきます。

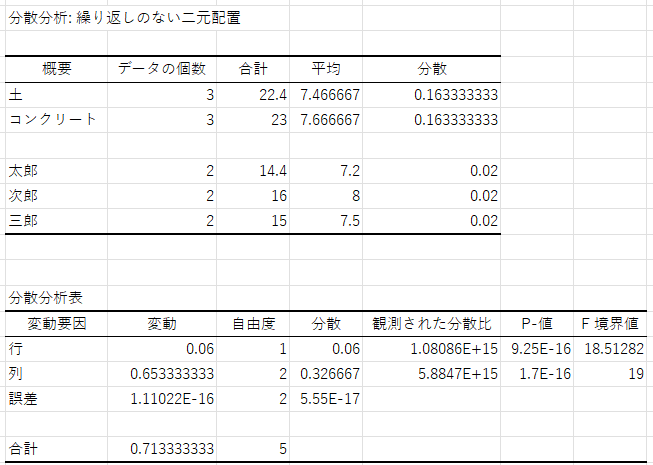
上の表は単純な集計です。

下の分散分析表は、一元配置分散分析の出力結果と比べると少しだけ行が増えています。

行は元データでいう「土」か「コンクリート」についてのデータを示しており、列は元データでいう「太郎、次郎、三郎」についての結果を示しています。

今回の場合、行も列もP値が0.05を大きく下回っているため、有意差があるといえます。

二元配置の分散分析（繰り返しあり）の場合

繰り返しありの場合も「データ分析」から進んでいきます。

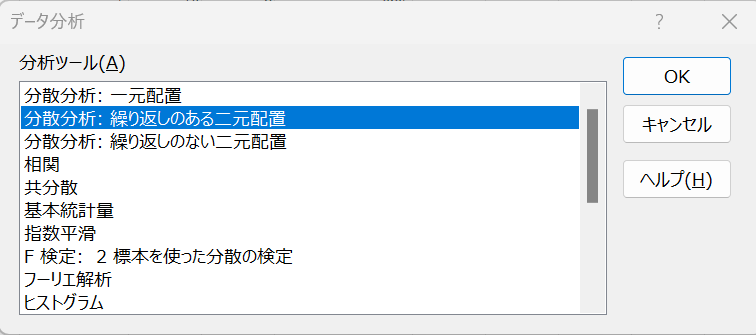
繰り返しのある二元配置の場合、以下のように「1標本あたりの行数」を入力する必要があるので入力します。

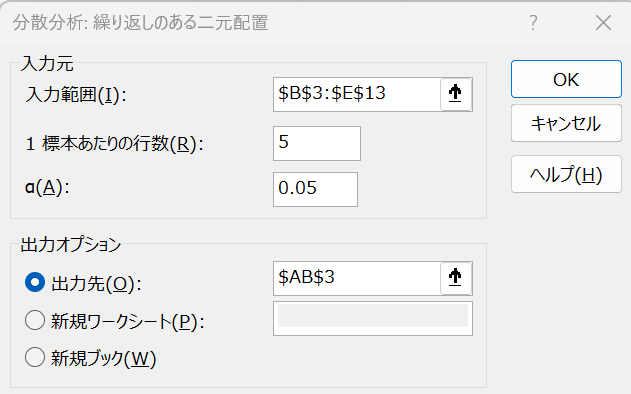
必要な情報を入力できたら「OK」をクリックします。

そうすると、以下のような分析結果が出力されます。

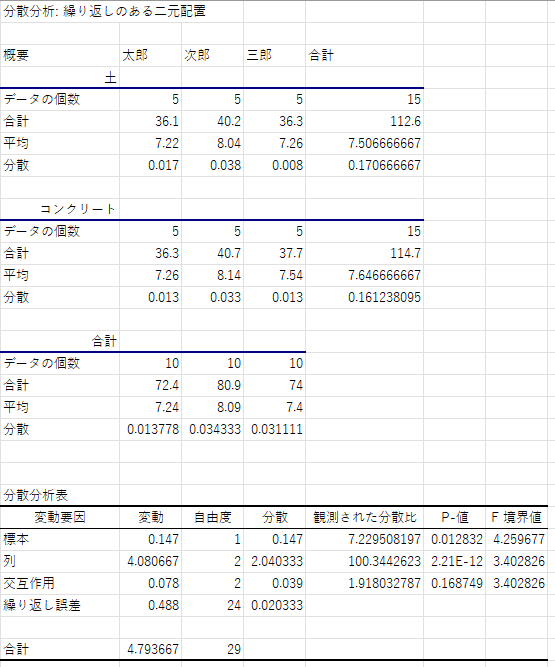
分散分析表以外の3つの表は単純な集計です。

分散分析表には、「標本」「列」「交互作用」という列が出てきています。

「標本」は元データの「土、コンクリート」で違い出ているかを表しており、「列」は「太郎、次郎、三郎」の間で差が出ているかを表しています。

今回の場合、標本も列もp値が0.05を下回っているので、有意差があるといえます。

また「交互作用」は、2つの要因が組み合わさることで現れる差をみています。

たとえば、太郎は土が得意で、次郎はコンクリートが得意、といったように組み合わせごとで有意な差があるか、といったイメージです。

今回、交互作用のP値は0.05を上回っているため、組み合わせによる有意な差はないと判断することができます。

ビジネスにおける分散分析の活用イメージ

次に、ビジネスにおいて分散分析をどのように活用していくのか、活用イメージをご紹介します。

ケース1　より発酵が上手くいく条件の組み合わせを探す

たとえば、納豆を製造している会社の場合を考えてみましょう。

納豆菌の種類を変えるだけ、室温を変えるだけでは発酵スピードに大きな変化はなかったとします。

しかし、それぞれ一つずつ変えるだけでは変化がなくても、2つの要因を一緒に変更してみると、発酵のスピードがより早く進むかもしれません。

そこで、納豆菌の種類と室温を一緒に変えた場合に最も発酵スピードが速い組み合わせを分散分析で考えることができます。

上記例は2元なので、2元配置分散分析を行うことになります。

もし、有意に発酵が早く進むような組み合わせを見つけることが出来れば、短い時間でさらに多くの納豆を作ることが出来るようになり、ビジネスの加速につながるかもしれません。

ケース2　喫煙習慣と血圧値の関係

分散分析を使えば、非喫煙者、喫煙者（一日20本未満）、喫煙者（一日20本以上）のグループに分類し、血圧を測定し、3つのグループで平均値に差があるか検定を行うといったことも可能です。

喫煙習慣と血圧に関連があることがみられれば、医師の場合それを治療にも生かすことが出来ます。

ケース3　職場環境による作業効率の差

たとえば、同じ会社のなかで、複数の工場で同じ製品を作っているというケースがあったとします。

そこで、異なる3つの職場環境で働く従業員に対して調査を行ない、職場環境により作業効率に与える差があるのかを分析することも可能です。

職場環境による作業効率において有意差がみつかれば、そこから先は何が要因になっているかを調べることで、職場環境の改善による作業効率の改善に繋げていくことができます。

まとめ

分散分析は、ビジネスの現場でもよく使われる分析手法の一つです。

とはいえ、相関分析のようになじみがあるものでもなく、少し統計学やデータ分析を学んだ人でないと知らない場合も多いと思います。

そのため、分散分析を知っているか知っていないかは、データ分析において差をつけることが出来る部分かと思います。

是非この機会に覚えておきましょう！

＼ この記事を読んだ方におすすめ！ ／