Z検定とは

Z検定は、平均値の差の検定という統計的検定手法の一つです。簡単にいうと、2つのグループ（群）の平均値が、等しいか、等しくないかを判定するときに使う分析手法です。

Z検定は、母分散が既に分かっている場合にのみ使われます（※母分散・・・母集団の分散。観測対象全体のデータのばらつき具合）。このことを「母分散σ²が既知である」といいます。

また、標準正規分布という確率分布を使っているというのもZ検定の特徴の一つです。

Z検定とt検定の違い

平均値の差の検定であるZ検定とt検定の違いについても説明します。

Z検定は母分散が既知である場合に使われる検定手法でした。

一方t検定は、母分散が不明（未知）な場合に使われる検定手法です。

つまり、母分散が既知か未知かで使い分けるということですね。

実務の場面では、母分散が分かっていることはあまり多くありません。

そのため、t検定の方がZ検定よりも汎用性が高い検定手法といえます。

t検定については、下記記事でExcelでの分析方法含め詳しく解説しているので、興味のある方は是非ご覧ください。

t検定とは Excelで分析を行う方法を解説

Z検定の方法

Z検定は、以下のような手順で進めていきます。

• 帰無仮説と対立仮説をたてる
• 有意水準を設定する
• 検定統計量（Z値）を算出する
• p値を求める
• 有意差を判定する

基本的な仮説検定のやり方と同じになります。

検定統計量のZ値とは、あるデータxが平均値μからどれだけ離れているかを標準偏差σで示した値のことです。

少し難しいですが、Z値というものを使って検定を行う、くらいの認識で大丈夫です。

また、p値とは、帰無仮説のもとでその事象が起こる確率のことです。

次章で紹介するExcelを使った分析方法の場合は、Z値もp値もまとめて算出してくれるので、スムーズに検定ができます。

Excelを使ったZ検定の手順

ここからは、ExcelでZ検定を行う方法について解説します。

Excelにデータ分析アドインが設定されている前提での進め方となりますので、まだの方は下記記事を参考に設定のうえ進めてください。

（参考）回帰分析とは　特徴やExcelでの分析方法を分かりやすく解説

今回は、以下のような「運動習慣の有無」と「BMI」のデータについてZ検定を行い、2グループの平均値に有意な差があるかどうかをみていきます。

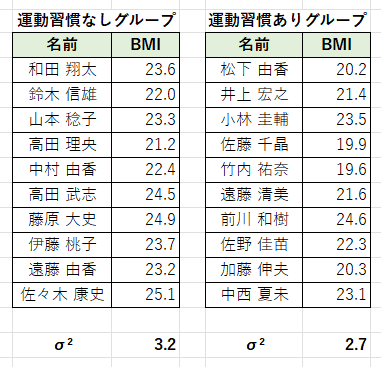
ちなみに、表の下に記載しているσ²はそれぞれのグループの母分散です。

「過去のデータから、あらかじめ母分散が既知である」という前提で進めていきます。

まずは、帰無仮説と対立仮説をたてていきます。

今回の場合は、「運動習慣の有無」と「BMIの平均値」の関係性を見ていきたいので、以下のような仮説を設定します。

• 帰無仮説：「運動習慣ありグループ」と「運動習慣なしグループ」のBMIの平均値に差がない
• 対立仮説：「運動習慣ありグループ」と「運動習慣なしグループ」のBMIの平均値に差がある

帰無仮説は、「否定したい仮説」のことです。

帰無仮説を否定することで、対立仮説を説明していくようなイメージを持っていただければ分かりやすいかと思います。（「差がない」を否定できれば、「差がある」といえる、というイメージです。）

まずは、「データ」→「データ分析」→「Z検定：2標本による平均の検定」と進んでいきます。

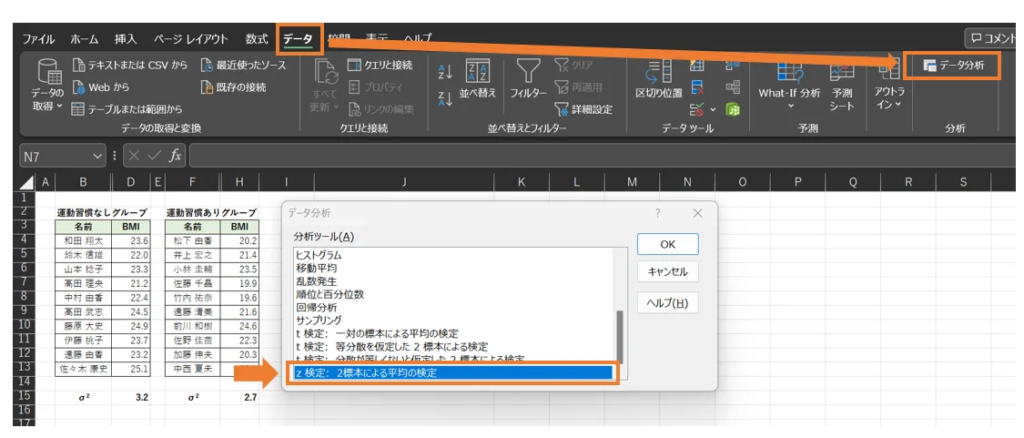
「OK」を押して、出てきたポップアップに必要な情報を入力していきます。

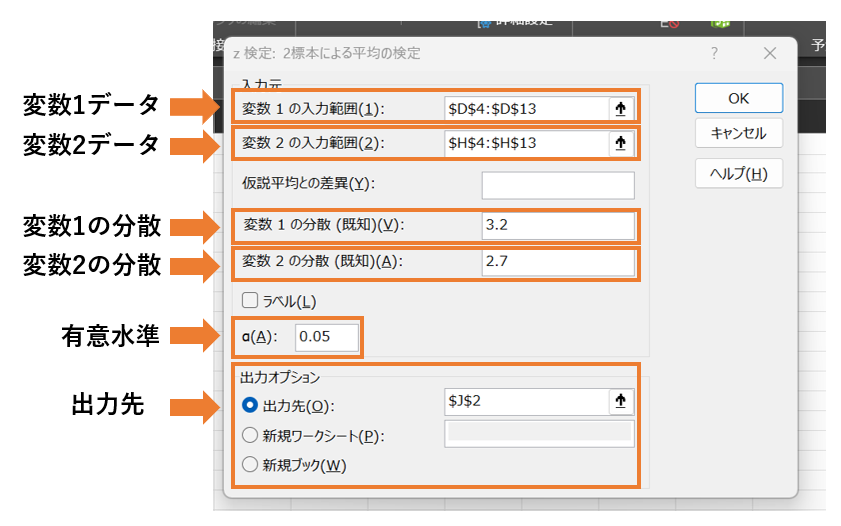
「変数1の入力範囲」「変数2の入力範囲」「変数1の分散」「変数2の分散」「α」「出力先」を入力していきます。

「α」は有意水準といい、p値と比べて有意差の有無を判断するための指標です。

多くの場合、5%(0.05)で設定することが多いです。

今回も有意水準は5％と設定し、進めていきます。

また、「仮説平均との差異」は空白のままでかまいません。

空白のままだと「2標本の平均値が同じであるかどうか」という帰無仮説を検定することになります。もし2標本の平均値の差が一定以上かどうかなどを検定したい場合にはその値を入れて使います。

今回は「2グループの平均値に差がない」ということを帰無仮説にしているため、空白のままで大丈夫です。

最後に出力先を選び、「OK」をクリックすると、以下のような分析結果が出力されます。

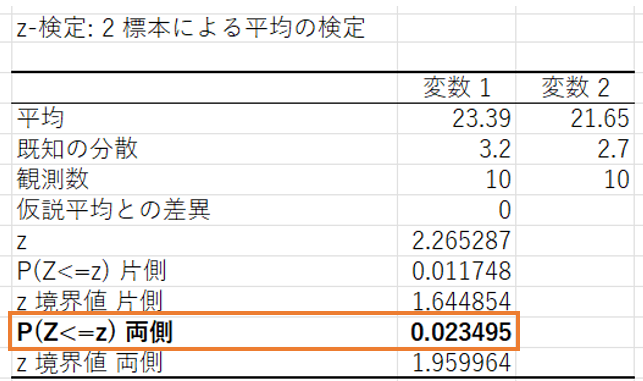
さて、出力データを読み取っていきましょう。

今回は、両側検定なので、「P（Z＜＝z）両側」のp値を確認していきます。

すると、p値は0.023495ということが分かります。

つまり、有意水準5％（0.05）よりも小さくなるため、帰無仮説は棄却し、対立仮説を採択していく、ということになります。

帰無仮説「「運動習慣ありグループ」と「運動習慣なしグループ」のBMIの平均値に差がない」を棄却するということは、つまり「運動習慣ありグループ」と「運動習慣なしグループ」のBMIの平均値には差があるといえるということです。

以上がZ検定の基本的な手順です。（今回用意したデータは解説用に作成したサンプルデータなので、実際に「運動習慣の有無」によって「BMIの平均値」に差が生じることを示すわけではありません）

Z検定の注意点

Z検定について詳しく紹介してきましたが、実はZ検定はあまり実用的な検定とはいえません。

というのも、Z検定を行うには、「母分散（母集団の分散）が既知である」という条件があります。

しかし、現実では母分散が既知なケースは稀で、母分散が分からない状態で分析をすることの方が多いです。

そのためビジネスの現場で使うことがあるかと聞かれると、あまりないというのが現実です。

ただし、Z検定は基本的な仮説検定のフローをしており、統計学初学者が仮説検定の基本的な流れを理解するためによく紹介されます。

実際、Z検定の流れを覚えておけば、t検定に対する理解もスムーズになると思います。

そのため、実用性は低いものの基本的な仮説検定という点で理解しておきたい検定といえます。

まとめ

Z検定はt検定と比べると使用頻度は少ないですが、知っておくことで仮説検定のイメージもつかみやすくなります。

是非この機会に覚えておきましょう。

＼ この記事を読んでいる人におすすめ！ ／