今回は統計学の学習時に出てくる「標準偏差」とは何なのか、どのようにして求めるのか、活用場面などをご紹介していきます。

標準偏差とは

標準偏差は、データのばらつきを表す指標の一つです。

「データのばらつき」というのは、平均からのはなれ具合のことです。

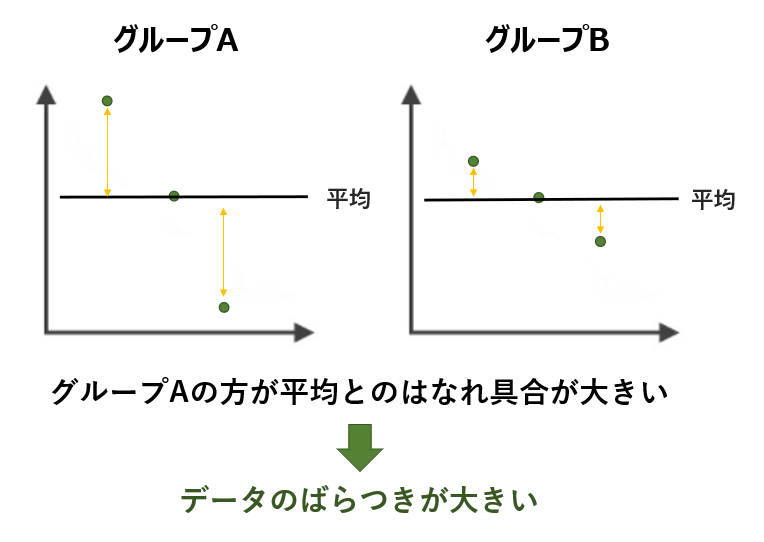
例えば、以下のような2つのデータがあったとします。

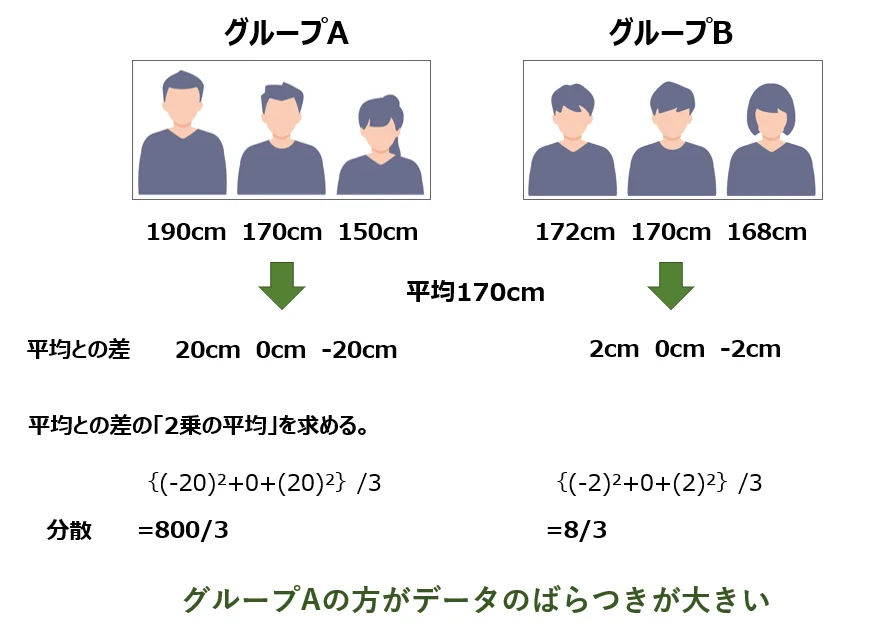
• グループAに属する3人の身長：150cm、170cm、190cm
• グループBに属する3人の身長：168cm，170cm、172cm

どちらのグループも、平均身長を算出すると170cmになります。

しかし、データの中身は全然違うというのは一目瞭然です。

特に、170cmという平均からAグループの方が離れている度合いが大きいというのが分かります。

これがデータのばらつきです。

平均値だけをみてもデータのばらつき具合までは分からないので、データのばらつきが分かる指標もあわせて確認することが重要です。

このようにデータのばらつきを数値化したものが標準偏差です。

標準偏差と密接な関係にある「分散」とは

標準偏差を知る上で重要なのが「分散」です。

というのも、標準偏差は「分散の平方根」を取った値だからです。

計算式でいうと、「標準偏差＝√分散」ということです。

そのため、分散もデータのばらつきを表す指標の一つです。

より具体的にいうと、分散は全データの平均からのはなれ具合を数値化したものです。

言葉だとわかりにくいので、まずは実際に分散を求めていきましょう。

分散、標準偏差の求め方

分散は、以下の計算式で求めることが出来ます。

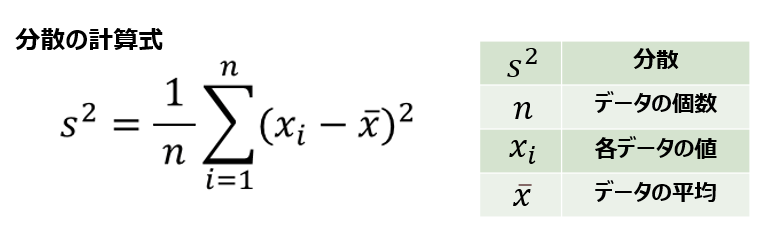
この式の意味は、「平均とのはなれ具合を求め、それを二乗し、その平均を求めている」という式です。

先ほど挙げた、身長の例で分散を考えてみます。

• グループAに属する3人の身長：190cm、170cm、150cm
• グループBに属する3人の身長：172cm，170cm、168cm

まず、グループAの各データについて「平均（170cm）とのはなれ具合」を求めると、それぞれ以下のようになります。

• 20、0、20

次に、この二乗を求めていきます。そうすると以下のようになります。

• 400、0、400

最後に、これらの平均を求めていきます。

そうすると、800/3となります。

これがグループAにおける平均身長の分散です。そして、こちらにルートをつけた√800/√3が標準偏差となります。

式だけみると難しそうですが、一つ一つ順を追って考えていくとシンプルですね。

同様に、グループBに属する3人の身長：172cm，170cm、168cmについて分散を求めると、8/3になります。こちらもルートをつけた√8/√3が標準偏差となります。

標準偏差は、大きければ大きいほどばらつきも大きいことを示します。

• グループAの標準偏差：√800/√3
• グループBの標準偏差：√8/√3

つまり、今回の場合は、グループAの方がデータのばらつきが大きいということが分かります。

ばらつきの大きさを数値化出来るというのが分散、標準偏差のよさですね。

標準偏差と分散の違い

ここまでの説明を聞いて、

「データのばらつきをみるだけなら、分散があればいいのでは？」

「なぜ分散にルートをつけた標準偏差という値があるの？」と思った方もおられるかもしれません。

その理由は、分散の計算過程にあります。

分散では、計算の過程で「平均とのズレを2乗」していました。

その理由は、そのままズレを足し引きした場合、平均との差なので、相殺し合ってプラマイ0になってしまうからです。それを防ぐために、2乗することでマイナスをプラスに変えています。

しかし、そのデメリットとして「二乗することにより単位も変わってしまう」のです。

たとえば、cm（センチメートル）の話をしているのに、分散はcm²（平方センチメートル）となってしまい、イメージしにくい値になってしまいます。

そのため二乗したぶん、ルートをつけることで元の単位に戻しています。

これが分散とは別で標準偏差が使われる理由です。

Excelで標準偏差を求める方法

ここからは、Excelで標準偏差を求める方法についても解説します。

標準偏差を求める際に使うのは、「STDEV.P」という関数です。

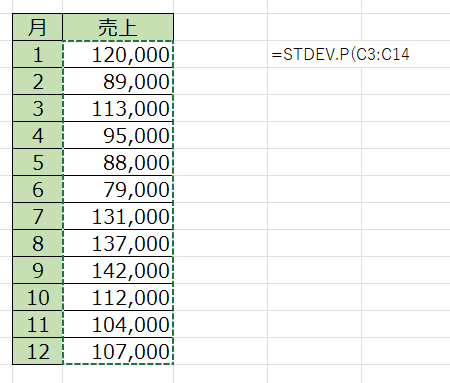
例として、以下のような月別の売上データがあるとしましょう。

この売上データのばらつきの大きさを知るために、標準偏差を求めていきます。

①まず「=STDEV.P」の関数を表示させます。

②売上金額のセルを選択します。

③標準偏差が表示されます。

これで、標準偏差は19283.5と求めることが出来ました。

手計算で求める時は少し大変でしたが、Excelだとこのように簡単に求めることができます。

ビジネスにおける標準偏差の活用事例

標準偏差は、ビジネスや日常においても活用されています。

売上分析

標準偏差は、各地域や店舗の売上のばらつきや安定性を測定する指標としても活用できます。

先ほどのExcelを使ったの例のように、月別の売上データを店舗ごとに集計し標準偏差を求めれば、各店舗における売上のばらつきを比較することができます。

具体的には、標準偏差が小さい場合、その店舗の売上は安定しており、一年を通して一定の売上を上げていることを示します。

逆に、標準偏差が大きい場合、月ごとに売上のばらつきが大きく、需要の不安定性がある可能性が高まります。

この情報を活用することで、在庫や人員の適切な配置などを検討することができます。

品質管理

製造業やサービス業において、製品やサービスの品質は重要な要素です。品質の評価においても、標準偏差は欠かせない指標です。

例えば、同じ製品を製造していても、品質のばらつきが大きい場合、一部の製品が規定の基準を満たしていない可能性があります。

このような場合には、製造プロセスや品質管理の改善が必要となるでしょう。

偏差値

受験のときによく聞く「偏差値」も標準偏差を活用した値の一つです。

偏差値は、学力などの検査結果が、集団の平均値からどの程度へだたっているかを示す数値です。

引用元：デジタル大辞泉

要するに、自分のとった点数が全体のなかでどれくらいに位置するのかを相対的に読み取るための指標というイメージを持っていただければと思います。

偏差値は、「{(得点－平均値)/標準偏差}×10＋50」という計算方法で求めることができます。

この式に含まれている平均や標準偏差はテストによって変わってくる値です。

そのため同じ点数の場合でも、テストによって偏差値も変わってきます。

まとめ

標準偏差、分散は、データのばらつきを表す指標です。

データのばらつきまで数値でだすことで、ばらつきの大きさを比較したり、評価することが出来るようになります。

また、平均値などでは読み取れなかったデータの特徴も把握出来るようになります。

ビジネスにおいても、グループごとに売上データや営業成績などばらつきをみてみるなど、標準偏差の活用方法はさまざまです。

標準偏差は、データ分析を学ぶうえで非常に重要な考え方ですので、是非覚えておきましょう。

＼ この記事を読んだ方におすすめ！ ／